Криволинейный интеграл первого рода. Свойства. Вычисление.

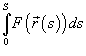Криволинейный интеграл — интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве.

Если на кривой C определена скалярная функция F, то интеграл называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C.

Свойства: Линейность:

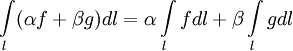
Аддитивность: если 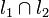в одной точке, то

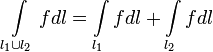
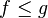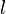Монотонность: если на , то

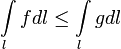
Теорема о среднем для непрерывной вдоль 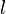функции :

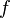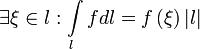
5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: .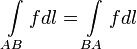

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

Вычисление: Пусть 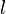— гладкая, спрямляемая кривая, заданная параметрически. Пусть функция 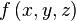определена и интегрируема вдоль кривой 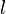в смысле криволинейного интеграла первого рода. Тогда

.

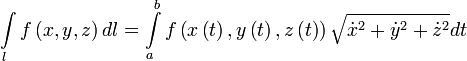Здесь точкой обозначена производная по 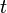: .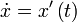