Методические указания. Уравнение, в которое входят производные искомой функции, называется дифференциальным уравнением

Уравнение, в которое входят производные искомой функции, называется дифференциальным уравнением. Уравнение, содержащее производную только первого порядка от одной переменой, называется обыкновенным дифференциальным уравнением первого порядка. Оно имеет общий вид

,

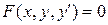где F – заданная функция трех переменных 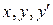; х – независимая переменная, 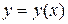искомая функция от х, 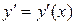– ее производная.

Простейшим дифференциальным уравнением первого порядка является уравнение вида

,

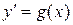где 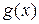– заданная функция. Имея ввиду, что 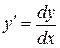, можно записать

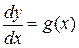, или .

Решение этого уравнения имеет вид ,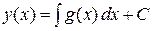

где С – произвольная постоянная.

Решение, содержащее произвольную постоянную, называется общим решением дифференциального уравнения.

Решение, в котором произвольная постоянная имеет определенное значение, обусловленное так называемыми начальными условиями, называется частным решением дифференциального уравнения.