
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 11. Найти общее решение дифференциального уравнения частное решение, удовлетворяющее условию .
|
|
Задача 11. Найти общее решение дифференциального уравнения 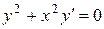 частное решение, удовлетворяющее условию
частное решение, удовлетворяющее условию 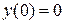 .
.
Решение. Перепишем данное уравнение, исходя из того, что 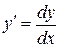 . Имеем
. Имеем 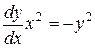 .
.
Данное уравнение является дифференциальным уравнением первого порядка с разделяющимися переменными. Чтобы разделить переменные, разделим обе части равенства на 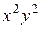 и умножим на
и умножим на 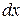 . Тогда
. Тогда
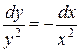 или
или 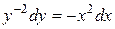 .
.
Интегрируя обе части уравнения 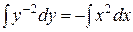 ,
,
получаем искомое общее решение 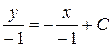 . или
. или 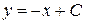 .
.
Частное решение найдем, подставляя в общее решение начальные значения х и у
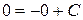 , то есть
, то есть 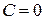 , и
, и 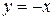 .
.
Задача 12. Найти общее решение дифференциального уравнения 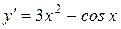 и частное решение, удовлетворяющее условию
и частное решение, удовлетворяющее условию 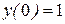 .
.
Решение. Перепишем данное уравнение, исходя из того, что 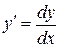 . Имеем
. Имеем 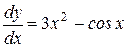 . Чтобы разделить переменные, умножим обе части равенства на
. Чтобы разделить переменные, умножим обе части равенства на 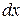 . Тогда
. Тогда 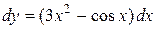 .
.
Интегрируя обе части уравнения 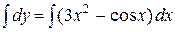 , получаем искомое общее решение
, получаем искомое общее решение 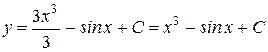 .
.
Частное решение мы найдем, подставляя в общее решение начальные значения х и у
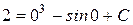 , то есть
, то есть 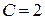 , и
, и 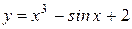 .
.
Вопросы для самопроверки
1.Сформулируйте определение дифференциального уравнения.
2. Какие уравнения называются дифференциальными уравнениями первого порядка?
3. Какое решение дифференциального уравнения называется общим; частным?