
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные формулы дифференцирования
|
|
1.  . 6.
. 6. 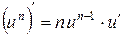 .
.
2. 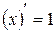 . 7.
. 7. 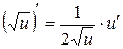 .
.
3. 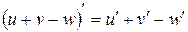 . 8.
. 8. 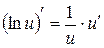 .
.
4. 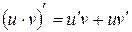 . 9.
. 9. 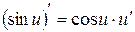 .
.
5. 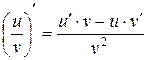 . 10.
. 10. 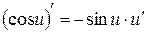
Рассмотрим примеры нахождения производных различных функций на конкретных примерах.
Задача 3. Найти производную функции
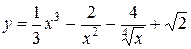 .
.
Решение. Преобразуем функцию у, введя степени с отрицательными и дробными показателями: 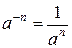 и
и 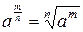 . Имеем:
. Имеем:
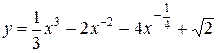 .
.
Применив формулу дифференцирования алгебраической суммы, получим:
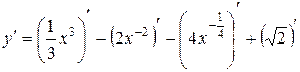 =
= 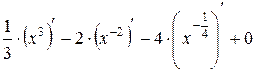 .
.
Затем по формуле дифференцирования степенной функции
 =
=
= 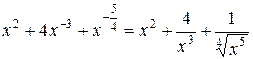 .
.
Задача 4. Найти производную функции
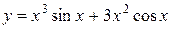 .
.
Решение. Применяя правила дифференцирования алгебраической суммы (3) и произведения (4), имеем
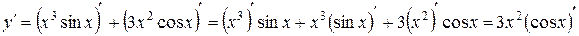 .
.
Далее по формулам (7), (12), (13) получаем
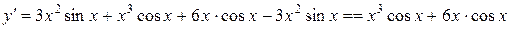 .
.
Вопросы для самопроверки
1. Дайте определение производной функции.
2. В чем заключается геометрический смысл производной?
3. Сформулируйте правила дифференцирования суммы, произведения, частного.
4. Сформулируйте правило дифференцирования сложной функции.
5. Что называется производной второго порядка?