
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Пусть система трех линейных уравнений с тремя неизвестными имеет вид
|
|
Пусть система трех линейных уравнений с тремя неизвестными имеет вид
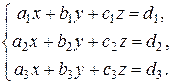
Решением данной системы называется такая тройка чисел (х; у; z), которая при подстановке в систему обращает каждое уравнение в верное равенство.
Для нахождения значений этой тройки чисел (х; у; z), метод Крамера использует так называемые определители системы уравнений.
В алгебре определителем квадратной таблицы чисел называется число, получаемое в результате определенной комбинации сложений и вычитаний произведений чисел таблицы, также производимых по определенным правилам. Например, простейшая квадратная система чисел содержит четыре числа
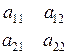 .
.
Первая цифра индекса числа указывает номер строки, на которой расположено данное число, второе число индекса – номер столбца, содержащего это число.
Определитель таблицы обозначается заглавной греческой буквой Δ, а таблица чисел в этом случае обозначается двумя вертикальными прямыми.
Для квадратной таблицы, содержащей четыре числа, определитель находится как разность произведения чисел, стоящих на диагонали, соединяющей числа 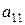 и
и 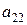 , (эта диагональ называется главной) и произведения чисел
, (эта диагональ называется главной) и произведения чисел 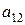 и
и 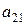 , стоящих на диагонали, называемой побочной
, стоящих на диагонали, называемой побочной
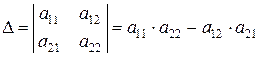 .
.
Следующей по размеру квадратной таблицей чисел является таблица, содержащая девять чисел
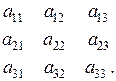
Определитель этой таблицы можно найти, используя свойство определителей, согласно которому определитель таблицы равен сумме произведений каждого из чисел первой строки на их алгебраические дополнения.
Алгебраическим дополнением какого-либо числа квадратной таблицы называется определитель таблицы, получаемый из этой таблицы вычеркиванием строки и столбца, на пересечении которых расположено данное число, умноженный на множитель 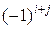 , где i – номер строки, а j – номер столбца, на пересечении которых расположено это число. Например, алгебраическое дополнение числа
, где i – номер строки, а j – номер столбца, на пересечении которых расположено это число. Например, алгебраическое дополнение числа 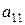
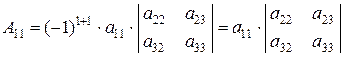 ,
,
соответственно, алгебраическое дополнение числа 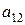
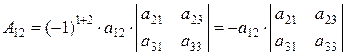 .
.
Тогда определитель квадратной таблицы размерностью 3х3 будет равен
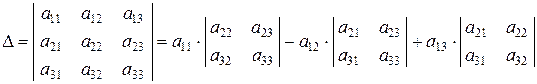 .
.
При решении системы трех линейных уравнений
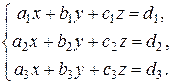
вначале находят главный определитель таблицы, состоящей из коэффициентов при неизвестных
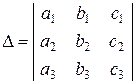 .
.
Вспомогательные определители системы получаются из главного определителя заменой соответствующего столбца столбцом свободных членов (обычно стоящих справа от знака равенства).
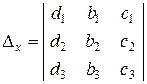 ;
; 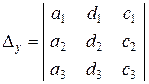 ;
; 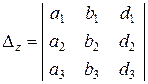 .
.
Если главный определитель системы не равен нулю, т.е. ∆ ≠ 0, то система (2) имеет единственное решение, которое находится по формулам Крамера:
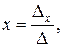
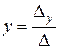 ,
, 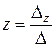 .
.
Если главный определитель системы равен нулю, т.е. ∆ = 0, а хотя бы один из вспомогательных не равен нулю, система (1) не имеет решений и называется несовместной.
Если главный определитель системы равен нулю, т.е. ∆ = 0, и все вспомогательные равны нулю, т.е. ∆ х = ∆ у = ∆ z = 0, то система (2) имеет бесконечное множество решений и называется неопределенной.
Рассмотрим конкретный пример.
Задача 2. Решить систему уравнений
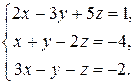
Решение. Составим квадратную таблицу главного определителя и найдем его
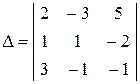 =
= 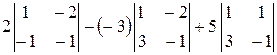 =
=
= 2(1∙ (-1) - (-1)∙ (-2)) + 3(1∙ (-1) - 3∙ (-2)) + 5(1∙ (-1) - 3∙ 1) = -6 + 15 - 20 = -11.
Теперь заменим числа первого столбца, числами соответствующих свободных членов уравнений и найдем вспомогательный определитель 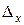
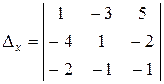 =
= 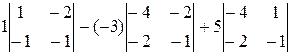 =
=
= (1∙ (-1) - (-1)∙ (-2)) + 3((-4)∙ (-1) – (-2)∙ (-2)) + 5((-4)∙ (-1) – (-2)∙ 1) =
= (-1-2) + 3(4-4) + 5(4+2) = -3 + 0 + 30 = 27.
Аналогично находим определители 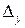 и
и 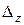 :
:
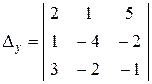 =45;
=45; 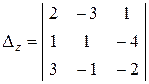 = 14.
= 14.
Очевидно, система имеет единственное решение.
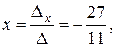
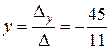 ,
, 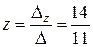 .
.