Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Аналитическая геометрия – это раздел математики, в котором изучают свойства геометрических объектов (точек
|
|
Аналитическая геометрия – это раздел математики, в котором изучают свойства геометрических объектов (точек, линий, поверхностей и тел) средствами алгебры и математического анализа при помощи метода координат.
Суть аналитической геометрии заключается в том, что геометрическим объектам сопоставляются уравнения или системы уравнений, так что их геометрические свойства выражаются в свойствах их уравнений. Благодаря этому можно находить длины отрезков, их ориентацию в пространстве, углы между ними, площади различных фигур и т. п., без построения чертежей с помощью линейки и циркуля, без измерения длин отрезков и углов между ними.
В аналитической геометрии наиболее широко используется так называемая декартова система координат, которая представляет собой две пересекающиеся под прямым углом оси, одна из которых направлена горизонтально слева направо и называется осью абсцисс, вторая – направлена снизу вверх, она перпендикулярна оси абсцисс и называется осью ординат. Точка пересечения осей обозначается буквой О и имеет нулевое значение как на оси абсцисс, так и на оси ординат.
Всю плоскость эти две оси разбивают на четыре части называемые четвертями или квадрантами (от латинского qwadro – четыре). Верхний правый квадрант называется первым, верхний левый – вторым, далее, двигаясь против часовой стрелки, – третий и четвертый. Любую точку М на плоскости можно определить двумя числами – расстояниями от этой точки до координатных осей. Эти числа называются координатами данной точки. Расстояние от точки М до оси ординат обозначается х, и называется абсциссой этой точки, расстояние до оси абсцисс обозначается у, и называется ординатой точки М.
Поэтому краткая запись положения точки на плоскости имеет вид М(х; у), где х и у некоторые числа.
 |
у 
М 2(х 2; у 2)
у 1 
N
М1 (х 1; у 1)
0 х 1 х 2 х
Рисунок 1 – Определение расстояния между двумя точками на плоскости
Если даны точки, М 1 и М 2, координаты которых известны, можно легко найти расстояние между ними. Как видно из рисунка 1, искомое расстояние это гипотенуза прямоугольного треугольника Δ М 1 М 2 N. По теореме Пифагора
.
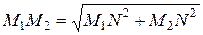В то же время, очевидно,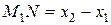 
, 
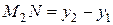. Тогда
.
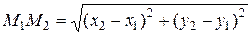Таким образом, используя формулы аналитической геометрии, можно найти уравнения прямых, координаты точек их пересечения, углы между ними и тому подобные характеристики геометрических объектов.
Задача 1. Координаты вершин треугольника А (–2; 5), В (10, –4), С (8, 10). Найти:
1) периметр треугольника АВС с точностью до 0, 01;
4) уравнение стороны АВ в общем виде и ее угловой коэффициент;
3) координаты точки пересечения медиан;
4) уравнение высоты CD;
Решение 1. По исходным данным построим чертеж исследуемого треугольника.
 |
Y
12
С
8
А
4 D Е
 |
-4 0 4 8 12 x
-4 В
Рисунок 2 – Исследуемый треугольник АВС
Периметр треугольника равен сумме длин его сторон:
P ∆ ABC = AB + BC + CA.
Длину каждой стороны треугольника находим по формуле расстояния между точками: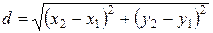 
.
.
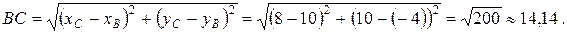
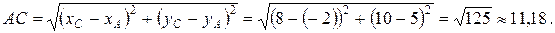
Итак: Р ∆ ABC = 15 + 14, 14 + 11, 18 ≈ 40, 32.
2. Уравнение прямой, проходящей через две точки А (x 1; y 1) и B (x 2; y 2), имеет вид: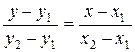 
. Подставим в это уравнение значения координат точек А и В
.
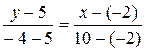Выполним преобразования
; 
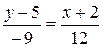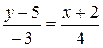; 4(y – 5) = -3(x + 2); 4 y – 20 = -3 x – 6,
отсюда общее уравнение прямой АВ: 3 x + 4 y – 14 = 0.
Для нахождения углового коэффициента прямой АВ приведем ее общее уравнение к виду y = k x + b:
4 y = -3 x + 14, 
, откуда kAB =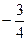 
.
3. Точка К пересечения медиан делит медиану АЕ в отношении λ = 2 ׃ 1, считая от вершины А. Точка Е – середина отрезка ВС. Найдем ее координаты, используя формулы:
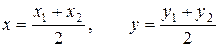
и подставляя в них координаты точек В и С:
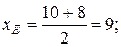
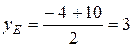. Следовательно, Е (9; 3).
По свойству точки пересечения медиан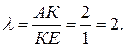 
Подставим значения координат и параметра λ в формулы:
Получаем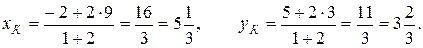 
Итак, точка пересечения медиан К (5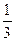 
; 3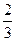 
).
4. Высота СD перпендикулярна стороне АВ, следовательно, их угловые коэффициенты удовлетворяют условию
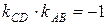, откуда 
.
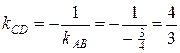Для составления уравнения высоты СD используем уравнение
y − y 0 = k ∙ (x − x 0 ).
Подставив значения координат точки С и угловой коэффициент k CD, получим уравнение высоты CD
y − 10 = 
(x − 8), откуда 3 (y − 10) = 4 (x − 8), или 4 x − 3 y − 2 = 0.
Вопросы для самопроверки
1. Напишите формулу для определения расстояния между двумя точками плоскости.
2. Напишите формулы для определения координат точки, делящей данный отрезок в данном отношении.
3. Напишите уравнение прямой, проходящей через две данные точки.
4. Какой вид имеет уравнение прямой с угловым коэффициентом?
5. В чем заключается геометрический смысл углового коэффициента?