Методические указания. Часто бывает необходимо найти функцию по ее известной производной

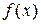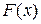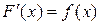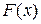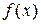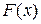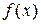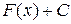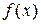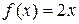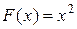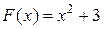Часто бывает необходимо найти функцию по ее известной производной. Если на интервале (а, b) для двух функций и справедливо соотношение , то называется первообразной для функции . При этом, если – первообразная для , то при любой постоянной С функция , также является первообразной для . Например, для функции , ее первообразная может иметь вид , или , или 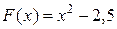, и т. п.

Неопределенным интегралом от функции 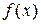называется общее выражение всех первообразных этой функции 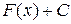. Он обозначается символом 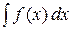и по определению

.

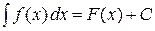Разумеется, 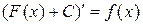. Выражение 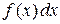называется подынтегральным выражением, а функция 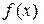– подынтегральной функцией.

Основные свойства неопределенного интеграла.

1. Дифференциал неопределенного интеграла равен подынтегральному выражению

.

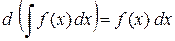2. Неопределенный интеграл от дифференциала некоторой функции отличается от этой функции на постоянную величину

.

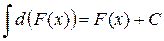3. Постоянный множитель можно выносить за знак неопределенного интеграла

.

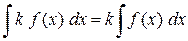4. Неопределенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме неопределенных интегралов от каждой функции в отдельности

.
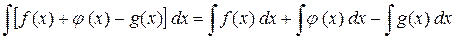