
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 8. Вычислить интеграл: .
|
|
Задача 8. Вычислить интеграл: 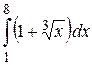 .
.
Решение. Используя свойства определенного интеграла, представим данный интеграл в виде суммы интегралов, для нахождения первообразных применяем табличный интеграл (1), а далее по формуле Ньютона – Лейбница вычисляем приращение первообразной.
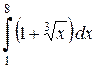 =
= 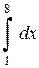 +
+ 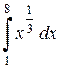 =
= 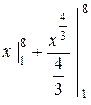 =
= 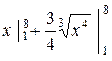 =
=
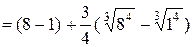
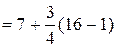 =
= 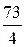 .
.
Задача 9. Вычислить интеграл: 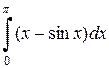 .
.
Решение. Используем свойства определенного интеграла, табличные интегралы (1) и (4), формулу Ньютона – Лейбница. Получаем
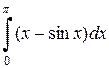 =
= 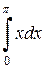 -
- 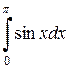 =
= 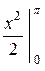 +
+ 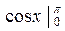 =
=
= 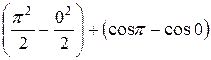 =
= 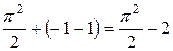 .
.
Задача 10. Найти площадь фигуры, ограниченной параболой 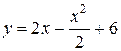 и прямой y = x + 2.
и прямой y = x + 2.
Решение. 1. Изобразим данные линии на чертеже и заштрихуем фигуру, площадь которой нужно найти. Графиком функции 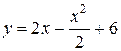 является парабола. Найдем производную данной функции и, приравняв ее к нулю, определим критическую точку
является парабола. Найдем производную данной функции и, приравняв ее к нулю, определим критическую точку 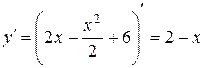 = 0. Отсюда х = 2. Это абсцисса вершины параболы. Ордината вершины
= 0. Отсюда х = 2. Это абсцисса вершины параболы. Ордината вершины 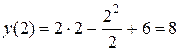 .
.
Найдем точки пересечения параболы с осью О х, положив у = 0. Тогда 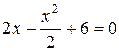 или
или 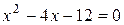 .
.
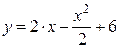
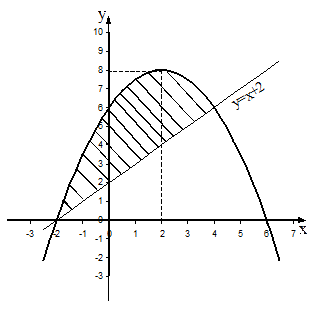
Рисунок 3 – Фигура, ограниченной параболой и прямой
Решив данное квадратное уравнение, получим х 1 = –2 и х 2 = 6. Строим параболу (рис. 3).
2. Графиком функции у = х + 2 является прямая, для ее построения достаточно двух точек. Положим х = 0, тогда у = 2. Положим х = 2, тогда у = 4. Строим прямую.
3. Площадь фигуры, ограниченной сверху непрерывной кривой 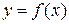 , снизу - непрерывной кривой
, снизу - непрерывной кривой 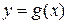 находится по формуле:
находится по формуле:
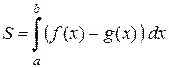 ,
,
где a и b – абсциссы точек пересечения кривых.
Для нахождения точек пересечения данных линий, решим систему уравнений:
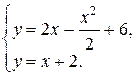
 , или
, или 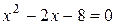 .
.
Решая полученное уравнение, получим х 1 = -2 и х 2 = 4, следовательно, а = -2; b = 4. Интеграл будет иметь вид
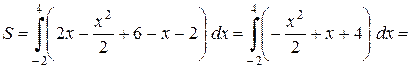
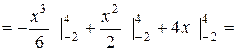
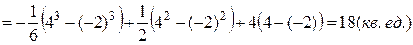 .
.
Вопросы для самопроверки.
1. Каков геометрический смысл определенного интеграла?
2. Сформулируйте свойства определенного интеграла.
3. Как вычисляется площадь плоской фигуры в прямоугольной системе координат?