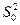Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однофакторный дисперсионный анализ.
|
|
В процессе эксперимента фактор Х поддерживают на n уровнях. На каждом i -ом уровне варьирования фактора проводят mi дублирующих экспериментов. Значение mi может быть одинаковым на уровнях или отличаться от уровня к уровню. Представим полученные результаты в виде таблицы 2.
Таблица 2. Представление результатов измерений для однофакторного дисперсионного анализа.
| № | Уровень фактора | Результаты измерений | Число дублирующих опытов |
| Х 1 |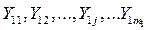 
| m 1 | |
| Х 2 | 
| m 2 | |
| … | … | … | … |
| i | Хi | mi | |
| … | … | … | … |
| n | Хn |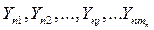 
| mn |
Рассеяние результатов измерения в одной строке определяется случайными погрешностями. Рассеяние между строками – дополнительным действием изучаемого фактора. Алгоритм расчета следующий.
1) Для каждой серии дублирующих опытов вычисляют оценки среднего арифметического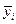 
и дисперсии воспроизводимости 
:
, 
2) Проверяют однородность ряда дисперсий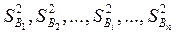 
для каждой пары. Если mi различно для каждого i, то при помощи критерия Фишера. При mi=m=const, то применяют критерий Кохрена. Если гипотеза однородности дисперсий подтверждается, то приступают к анализу.
3) Делаем допущения, что результат любого измерения 
, где μ – средняя арифметическая всех 
измерений,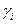 
- погрешность, определяемая влиянием контролируемого фактора, 
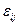- погрешность, вызванная случайными факторами.
4) Влияние случайных факторов 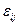оценивается средней дисперсией воспроизводимости:
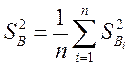
5) Влияние на рассеивание значений отклика совместного действия контролируемых и случайных факторов оценивается полной дисперсией:
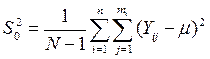, где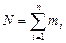 
; 
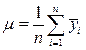
6) Влияние на рассеивание значений отклика контролируемого фактора оценивается дисперсией:
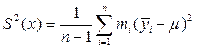
7) Проверяем однородность дисперсий
и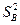 
:
7.1.) Вычисляем наблюдаемое значение критерия Фишера: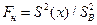 
7.2.) Вычисляем число степеней свободы m 1 и m 2
7.3.) Задаем доверительную вероятность Р.
7.4.) Находим критическое значение критерия Фишера F к при заданных степенях свободы. Если F н> Fк, то влияние фактора существенно. Тогда считается, что есть n нормально распределенных совокупностей, каждая из которых имеет одну и ту же дисперсию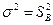 
и соответствующее математическое ожидание .
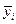Оценку дисперсии средних значений, вызванную влиянием исследуемого фактора Х, производят по формуле:
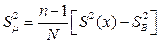
Если F н< F к (для заданных Р, m 1 и m 2), то влияние фактора Х несущественно и все результаты измерений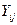 
относятся к одной генеральной совокупности, имеющей среднее арифметическое μ и дисперсию 