Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства криволинейного интеграла второго рода.
|
|
1) При смене ориентации кривой на противоположный криволинейный интеграл второго рода меняет знак, т.е. если кривая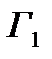 
отличается от кривой Г только ориентацией, символически 
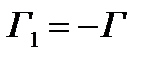, то для любого векторного поля G:
2) Аддитивность. Пусть точка С на кривой (ориентированной кривой) Г делит его на две кривых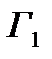 
и 
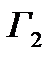с той же ориентацией, т.е., символически 
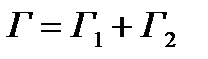, то
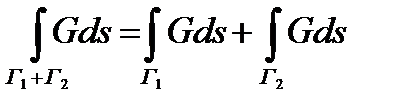
(точнее, если существуют оба интеграла в правой части, то существует интеграл, стоящий слева и равен выражению, стоящему справа).
3) Линейность. Для любых чисел из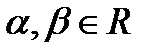 
и векторных полей F и G справедливо равенство:
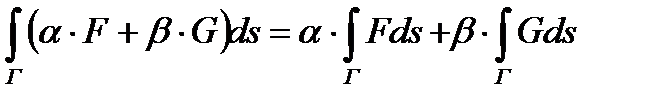
(точнее, если существуют оба интеграла в правой части, то существует интеграл, стоящий слева и равен выражению, стоящему справа).
4) Теорема об оценке. Если кривая Г имеет длину L, и в любой точке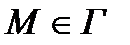 
для векторного поля G (M) справедливо неравенство
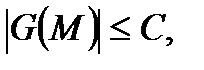
то справедлива оценка
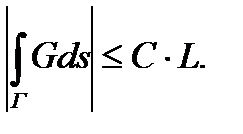
5) Связь с криволинейным интегралом первого рода. Пусть в любой точке 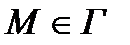векторное поле G (M) образует с касательным вектором к ориентированной кривой в этой точке угол 
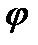(вообще говоря, зависящим от точки М), то
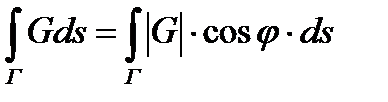
(слева стоит криволинейный интеграл второго рода, а справа - первого).