Связь криволинейных интегралов первого и второго рода.

Пусть на плоской кривой Г даны две произвольные точк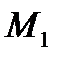и и 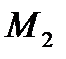(см. рис. 14). Обозначим через 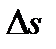длину кривой между точкам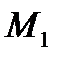и и 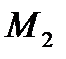, через 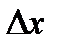- абсциссу вектора 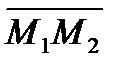, а через 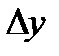- его ординату. Из криволинейного треугольника 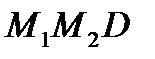(см. рис. 14) по теореме Пифагора получаем: 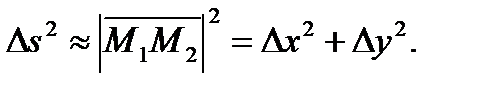Пусть 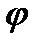- угол между вектором 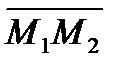и осью абсцисс, а 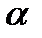- угол между касательной к кривой Г в точке 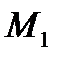(предельным направлением вектора 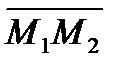при 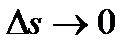) и положительным направлением оси. Тогда при 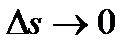имеем 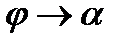. Кроме того, при малом значении 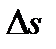можно считать, что 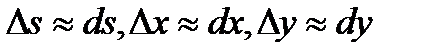. Поскольку 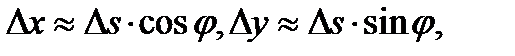то при 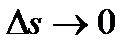получаем:

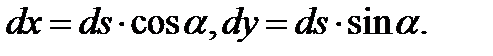
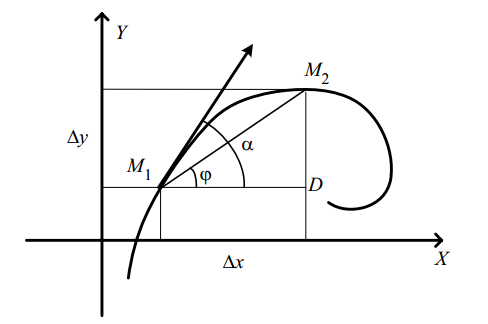
Рис.14. К выводу формулы связи криволинейных

интегралов первого и второго рода.

В случае пространственной кривой касательная в точке 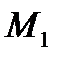(предельное положение луча, направленного по вектору 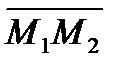образует с координатными осями OX, OY, и OZ углы 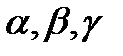, соответственно, а вектор 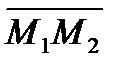образует с теми же осями