Вычисление криволинейного интеграла второго рода.

1) Основная формула для вычисления криволинейного интеграла второго рода, по сути, содержится во второй формой записи этого интеграла:

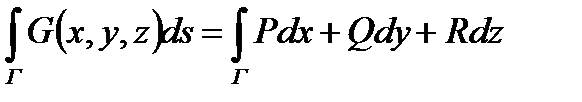
А именно, пусть в пространстве задана параметризация кривой

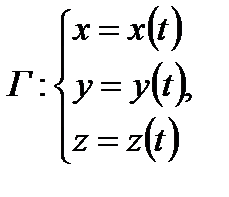
причем, заданная ориентация на Г соответствует изменению параметра t от 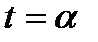и 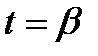(возможно также, что 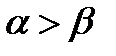). Тогда и

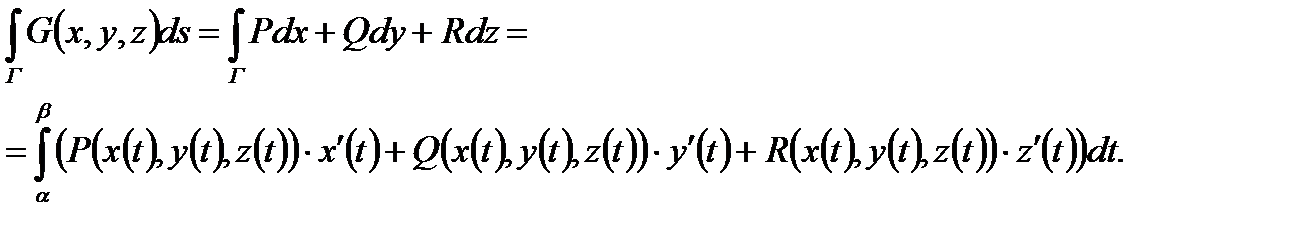
(4)

2) В случае " двумерного" криволинейного интеграла второго рода данная формула вычисления выглядит уже не так громоздко:

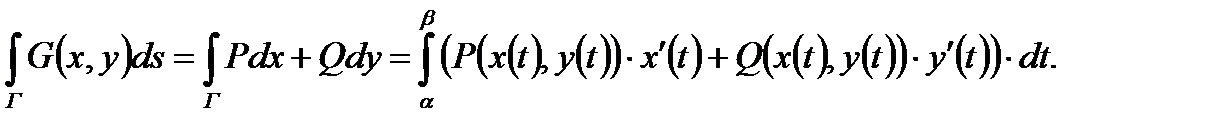
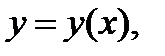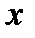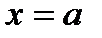3) Следующее формулы являются частными случаями предыдущих. Например, если на плоскости кривой Г задан явно: причем, ориентация кривой соответствует изменению от до 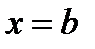(возможно, что a< b) то в качестве параметра выступает 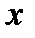, и предыдущая формула принимает такой вид:

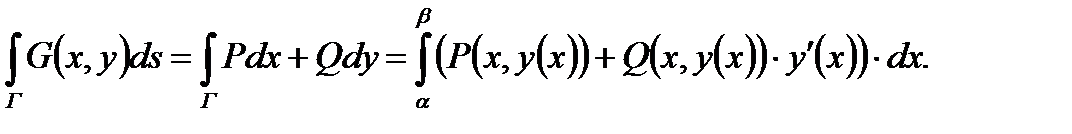
4) Если же ориентированная кривая Г задана на плоскости в полярных координатах:

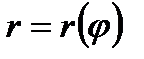, где 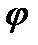изменяется от 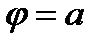до 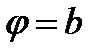, то надо подставить формулы

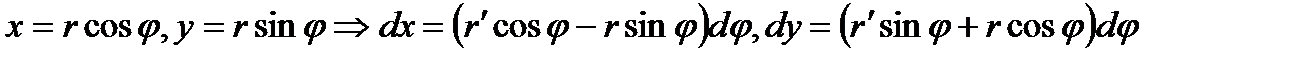
И поэтому формула для вычислений криволинейного интеграла второго рода в полярных координатах принимает такой вид:

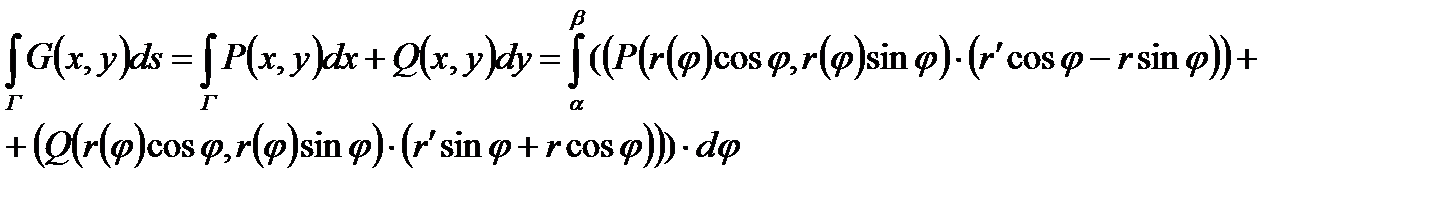
Замечание. Часто путем интегрирования (или его частью) в криволинейном интеграле являются отрезок кривой. Если начало и конец отрезка расположены соответственно в

точках 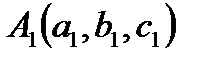и 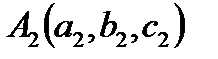, то отрезок 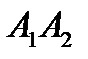задаётся параметрическими уравнениями:

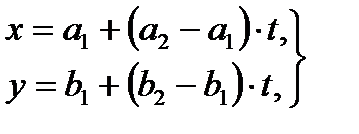
(5)

причем t изменяется от 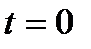(точка 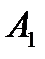) до 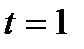(точка ).

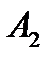ПРИМЕР 1. Найти работу векторного поля 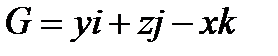вдоль одного витка винтовой кривой Г: 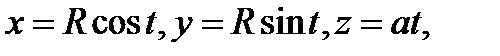направление от точки 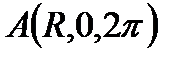до точки (см. рис. 13).

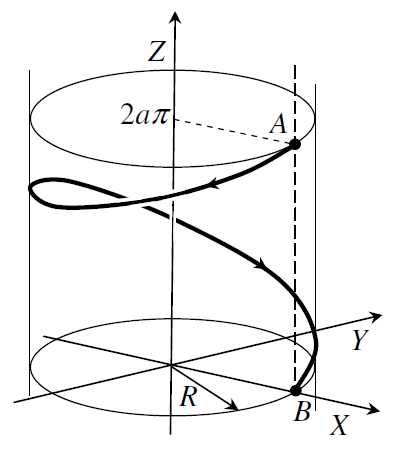
Рис.13. К примеру 1.

Ориентация кривой Г соответствует убыванию параметра t от 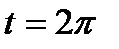до 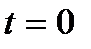. По формуле (4), искомая работа равна: