Случайная величина X распределена нормально и имеет плотность вероятности

f(x)= 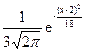. Дисперсия случайной величины Y=2X равна:

1) 6; 2) 36; 3) 18; 4) 16.

91. Случайная величина X распределена нормально и имеет плотность вероятности f(x)= 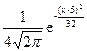. Математическое ожидание случайной величины Y=2X-3 равно:

1) 5; 2) 7; 3) 29; 4) 10.

92. Случайная величина подчинена нормальному закону с плотностью вероятности f(x)= 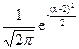. Дисперсия случайной величины Y=3X равна:

1) 6; 2) 12; 3) 9; 4) 15.

93. Случайная величина X имеет нормальное распределение, MX==2, DX=9.

Вероятность P(|X–MX|< 2) равна:

1) 0, 5148; 2) 0, 4972; 3) 0, 523; 4) 0, 4161.

94. Случайная величина X имеет нормальное распределение, MX==3, DX=4. Вероятность

P(|X–MX|< 6) равна:

1) 0, 9973; 2) 0, 9881; 3) 0, 9673; 4) 0, 9821.

95. Случайная величина X имеет нормальное распределение MX==30, DX=100. Вероятность P(20< X< 50) равна:

1) 0, 1359; 2) 0, 4215; 3) 0, 8185; 4) 0, 8541.

96. Случайная величина X имеет нормальное распределение с плотностью вероятности f(x)= . Дисперсия случайной величины Y=2X+1 равна:

1) 17; 2) 9; 3) 7; 4) 16.

97. Плотность вероятности случайной величины X, распределенной по показательному закону с параметром λ =5, имеет вид:

1) f(x)=λ ·e^{λ x}; 2) f(x)= ;

3) f(x)= 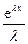; 4) f(x)= .

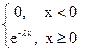98. Случайная величина X имеет показательное распределение f(x)=5e^-5x при x≥ 0, f(x)=0 при x< 0. P(0, 4< X< 1) равна:

1) 0, 13; 2) 0, 21; 3) 0, 75; 4) 0, 31.

99. Случайная величина X имеет показательное распределение f(x)= 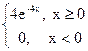. Математическое ожидание X равно:

1) MX= 4; 2) MX= 0, 5; 3) MX= 0, 25; 4) MX= - 0, 25.

100. Случайная величина X имеет показательное распределение f(x)= 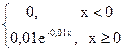. Математическое ожидание и среднее квадратичное отклонение MX, σ x равно:

1) MX=100; σ x=10; 2) MX=0, 01; σ x=100;

3) MX=100; σ x=100; 4) MX=0, 1; σ x=0, 1.