
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 3. Тфкп, операционное исчисление.
|
|
101. Корень квадратного уравнения z2+4=0 есть
1) нет решения;
2) 2j; –2j;
3) 2; –2.
102Корень квадратного уравнения z2+9=0 есть
1) нет решения;
2) 3j; –3j;
3) 3; –3.
103. Корень квадратного уравнения z2+1=0 есть
1) j; –j;
2) 1; –1;
3) нет решения.
104. Корень квадратного уравнения z2+16=0 есть
1) 4j; –4j;
2) 4; –4;
3) нет решения.
105. Корень квадратного уравнения z2+25=0 есть
1) 5j; –5j;
2) 5; –5;
3) нет решения.
106. Корень квадратного уравнения z2+49=0 есть
1) 7j; –7j;
2) 7; –7;
3) нет решения.
107. Корень квадратного уравнения z2+64=0 есть
1) 8; –8;
2) 8j; –8j;
3) нет решения.
108. Корень квадратного уравнения z2+81=0 есть
1) 9j; –9j;
2) 9; –9;
3) нет решения.
109. Корень квадратного уравнения z2+100=0 есть
1) нет решения;
2) 10; –10;
3) 10j; –10j.
110. Корень квадратного уравнения z2+121=0 есть
1) 11j; –11j;
2) 11; –11;
3) нет решения.
111. Алгебраическая форма 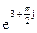 есть:
есть:
1) 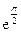 (cos3+j sin3);
(cos3+j sin3);
2) e3(cos 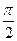 +j sin
+j sin 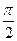 );
);
3) – e3(cos 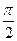 –j sin
–j sin 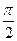 ).
).
112Алгебраическая форма  есть:
есть:
1) 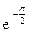 (cos3+j sin3);
(cos3+j sin3);
2) e3(cos 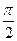 +j sin
+j sin 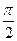 );
);
3) e3(cos 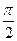 –j sin
–j sin 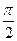 ).
).
113Алгебраическая форма 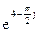 есть:
есть:
1) e4(cos 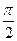 –j sin
–j sin 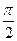 );
);
2) e4(cos 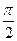 +j sin
+j sin 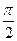 );
);
3) 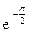 (cos4+j sin4).
(cos4+j sin4).
114Алгебраическая форма eπ j+4 есть:
1) e4(cosπ –jsinπ);
2) e4(cosπ +jsinπ);
3) eπ (cos4+jsin4).
115Алгебраическая форма 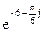 есть:
есть:
1) e–6(cos 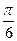 –j sin
–j sin 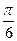 );
);
2) e–6(cos 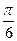 +j sin
+j sin 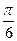 );
);
3) 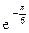 (cos6–j sin6).
(cos6–j sin6).
116Алгебраическая форма 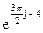 есть:
есть:
1) 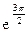 (cos4–j sin4);
(cos4–j sin4);
2) e4(cos 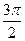 +j sin
+j sin 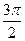 );
);
3) e–4(cos 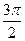 +j sin
+j sin 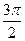 ).
).
117Алгебраическая форма 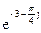 есть:
есть:
1) e–3(cos  –j sin
–j sin  );
);
2) e–3(cos  +j sin
+j sin  );
);
3) 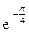 (cos3–j sin3).
(cos3–j sin3).
218Алгебраическая форма 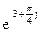 есть:
есть:
1) 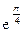 (cos3+j sin3);
(cos3+j sin3);
2) e3(cos  +j sin
+j sin  );
);
3) e3(cos  –j sin
–j sin  ).
).
119Алгебраическая форма 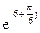 есть:
есть:
1) e6(cos 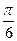 –j sin
–j sin 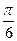 );
);
2) 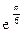 (cos6+j sin6);
(cos6+j sin6);
3) e6(cos 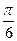 +j sin
+j sin 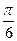 ).
).
120Алгебраическая форма 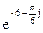 есть:
есть:
1) e–6(cos 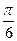 +j sin
+j sin 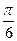 );
);
2) e–6(cos 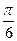 –j sin
–j sin 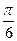 );
);
3) 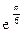 (cos6–j sin6).
(cos6–j sin6).
Алгебраическая форма 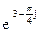 есть:
есть:
1) e3(cos  +j sin
+j sin  );
);
2) e3(cos  –j sin
–j sin  );
);
3) 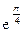 (cos3+j sin3).
(cos3+j sin3).
122Алгебраическая форма 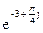 есть:
есть:
1) 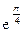 (cos3–j sin3);
(cos3–j sin3);
2) e–3(cos  –j sin
–j sin  );
);
3) e–3(cos  +j sin
+j sin  ).
).
123Алгебраическая форма 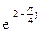 есть:
есть:
1) e2(cos  –j sin
–j sin  );
);
2) e2(cos  +j sin
+j sin  );
);
3) 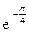 (cos2+j sin2).
(cos2+j sin2).
124Алгебраическая форма e –j есть:
1) cos1–j sin1;
2) e –j;
3) cos1+j sin1.
125Алгебраическая форма e 2+j есть:
1) e(cos2+j sin2).
2) e 2;
3) e2(cos1+j sin1).
126Алгебраическая форма e 2–j есть:
1) e2(cos1–j sin1);
2) e2(cos1+j sin1);
3) e–j(cos2+j sin2).
127Алгебраическая форма e j есть:
1) e;
2) cos1+j sin1;
3) cos1–j sin1.
128Алгебраическая форма  есть:
есть:
1) 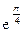 (cos2–j sin2).
(cos2–j sin2).
2) e–2(cos  –j sin
–j sin  );
);
3) 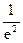 (cos
(cos  +j sin
+j sin  ).
).
129Алгебраическая форма 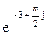 есть:
есть:
1)  (cos
(cos 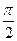 +j sin
+j sin 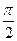 );
);
2) e–3(cos 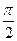 –j sin
–j sin 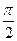 );
);
3) 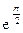 (cos3–j sin3).
(cos3–j sin3).
130Алгебраическая форма 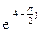 есть:
есть:
1) e3(cos 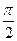 +j sin
+j sin 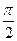 );
);
2) e4(cos 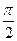 –j sin
–j sin 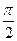 );
);
3) 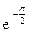 (cos4+j sin4).
(cos4+j sin4).
131Найти вычеты в особых точках:
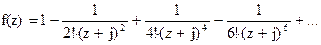
1) 1;
2) 0;
3) – 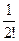 .
.
132Найти вычеты в особых точках:

1) 1;
2) –1;
3) 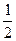 ;
;
4) 0.
Найти вычеты в особых точках: 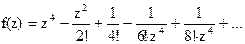
1) 1;
2) 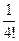 ;
;
3) 0.
134Найти вычеты в особых точках: 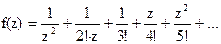
1) 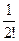 ;
;
2) 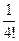 ;
;
3) 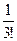 .
.
135Найти вычеты в особых точках: 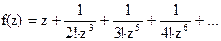
1) 1;
2) 0;
3) 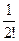 .
.
136Найти вычеты в особых точках: 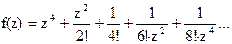
1) 1;
2) 0;
3) 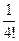 .
.
137Найти вычеты в особых точках: 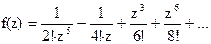
1) 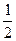 ;
;
2) 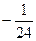 ;
;
3) 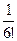 .
.
138Найти вычеты в особых точках: 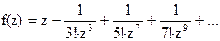
1) 0;
2) 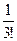 ;
;
3) 1.
139Найти вычеты в особых точках: 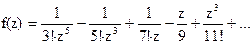
1) 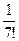 ;
;
2) 0;
3) – 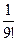 .
.
140Найти вычеты в особых точках: 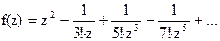
1) 1;
2) 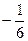 ;
;
3) 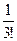 .
.
141Найти вычеты в особых точках: 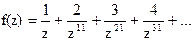
1) 1;
2) 2;
3) 0.
142Найти вычеты в особых точках: 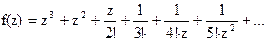
1) 1;
2) 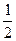 ;
;
3) 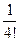 .
.
143Найти вычеты в особых точках: 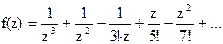
1) 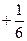 ;
;
2) 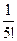 ;
;
3) – 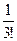 .
.
144Найти вычеты в особых точках: 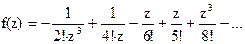
1) 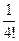 ;
;
2) 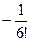 ;
;
3) 0.
145Найти вычеты в особых точках: 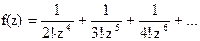
1) 0;
2) 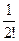 ;
;
3) 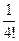 .
.
146Найти вычеты в особых точках: 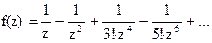
1) 1;
2) –1;
3) 0.
147Найти вычеты в особых точках: 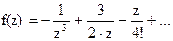
1) 0;
2) 3;
3) 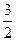 .
.
148Найти вычеты в особых точках: 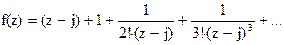
1) 1;
2) j;
3) 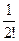 .
.
149Найти вычеты в особых точках: 
1) 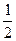 ;
;
2) 0;
3) 2!.
150Найти вычеты в особых точках: 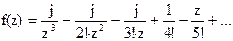
1) 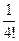 ;
;
2) 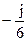 ;
;
3) 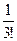 .
.
151Найти вычеты в особых точках: 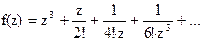
1) 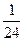 ;
;
2) 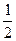 ;
;
3) 0.
152Найти вычеты в особых точках: 
1) 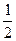 ;
;
2) 0;
3) – 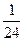 .
.
153Найти вычеты в особых точках: 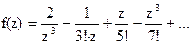
1) 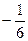 ;
;
2) 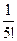 ;
;
3) 0.
154Найти вычеты в особых точках: 
1) 1;
2) – 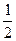 ;
;
3) 0.
155Найти вычеты в особых точках: 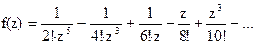
1) – 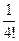 ;
;
2) 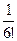 ;
;
3) – 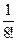 .
.
156Определить характер особых точек: 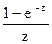 =
= 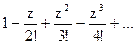
1) z=0 – устранимая особая точка;
2) z=0 – существенно особая точка;
3) z=0 – простой полюс.
157Определить характер особых точек:  =
= 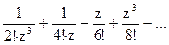
1) z=0 – полюс І порядка;
2) z=0 – простой полюс;
3) z=0 – полюс ІІІ порядка.
158Определить характер особых точек:
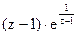 =
= 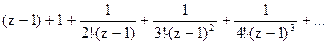
1) z=1 – устранимая особая точка;
2) z=1 – существенно особая точка;
3) z=1 – простой полюс.
159Определить характер особых точек:  =
= 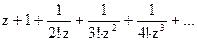
1) z=0 – существенно особая точка;
2) z=0 – устранимая особая точка;
3) z=0 – простой полюс.
160Определить характер особых точек: 
1) z=1 – полюс ІІІ порядка
z= –j – полюс ІІ порядка;
2) z= –1 –полюс ІІІ порядка
z=j – полюс ІІ порядка;
3) z=1 – полюс ІІІ порядка
z=j – полюс ІІ порядка.
161Определить характер особых точек: 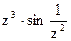 =
= 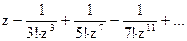
1) z=0 – существенно особая точка;
2) z=0 – устранимая особая точка;
3) z=0 – простой полюс.
162Определить характер особых точек: 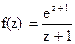
1) z=1 – существенно особая точка;
2) z=1 – простой полюс;
3) z= –1 – простой полюс.
163Определить характер особых точек: 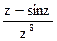 =
= 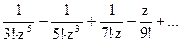
1) z=0 – простой полюс;
2) z=0 – полюс VIII порядка;
3) z=0 – полюс V порядка.
164Определить характер особых точек: 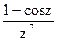 =
= 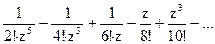
1) z=0 – полюс V порядка;
2) z=0 – полюс VII порядка;
3) z=0 – существенно особая точка.
165Определить характер особых точек: 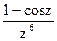 =
= 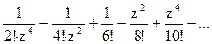
1) z=0 – существенно особая точка.
2) z=0 – полюс VI порядка;
3) z=0 – полюс IV порядка;
166Определить характер особых точек: 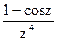 =
= 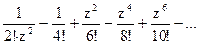
1) z=0 – полюс II порядка;
2) z=0 – полюс IV порядка;
3) z=0 – существенно особая точка.
167Определить характер особых точек: 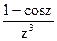 =
= 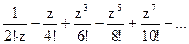
1) z=0 – полюс III порядка;
2) z=0 – простой полюс;
3) z=0 – устранимая особая точка.
168Определить характер особых точек:  =
= 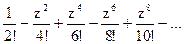
1) z=0 – существенно особая точка;
2) z=0 – полюс II порядка;
3) z=0 – устранимая особая точка.
169Определить характер особых точек:
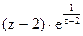 =
= 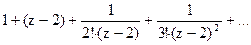
1) z=2 – существенно особая точка;
2) z=2 – устранимая особая точка;
3) z=2 – простой полюс.
170Определить характер особых точек:
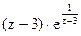 =
= 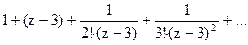
1) z=3 – устранимая особая точка;
2) z=3 – существенно особая точка;
3) z=3 – простой полюс.
171Определить характер особых точек:
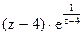 =
= 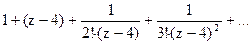
1) z=4 – простой полюс.
2) z=4 – устранимая особая точка;
3) z=4 – существенно особая точка;
172Определить характер особых точек:
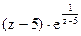 =
= 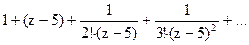
1) z=5 – существенно особая точка;
2) z=5 – устранимая особая точка;
3) z=5 – простой полюс.
173Определить характер особых точек: 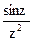 =
= 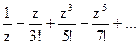
1) z=0 – существенно особая точка;
2) z=0 – простой полюс;
3) z=0 – полюс II порядка.
174Определить характер особых точек:
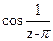 =
= 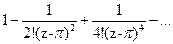
1) z= –π – существенно особая точка;
2) z= –π – устранимая особая точка;
3) z=π – существенно особая точка.
175Определить характер особых точек:
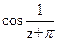 =
= 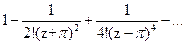
1) z=π – существенно особая точка;
2) z= –π – существенно особая точка;
3) z=π – устранимая особая точка.
176Определить характер особых точек:
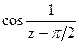 =
= 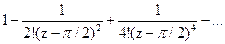
1) z=π /2 – устранимая особая точка;
2) z= –π /2 – существенно особая точка;
3) z=π /2 – существенно особая точка.
177Определить характер особых точек: 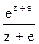
1) z= –e – простой полюс;
2) z=e – простой полюс;
3) z= –e – существенно особая точка.
178Определить характер особых точек: 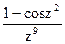 =
= 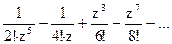
1) z=0 – полюс IX порядка;
2) z=0 – полюс V порядка;
3) z=0 – простой полюс.
179Определить характер особых точек: 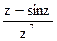 =
= 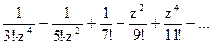
1) z=0 – полюс IV порядка;
2) z=0 – полюс VII порядка;
3) z=0 – устранимая особая точка.
180Определить характер особых точек: 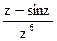 =
= 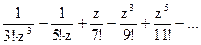
1) z=0 – простой полюс;
2) z=0 – полюс VI порядка;
3) z=0 – полюс III порядка.

181Определить характер особых точек: 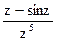 =
= 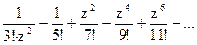
1) z=0 – полюс II порядка;
2) z=0 – полюс V порядка;
3) z=0 – простой полюс.
182Определить характер особых точек:  =
= 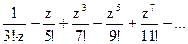
1) z=0 – полюс IV порядка;
2) z=0 – простой полюс;
3) z=0 – полюс III порядка.
183Определить характер особых точек: 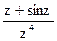 =
= 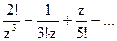
1) z=0 – полюс I порядка.
2) z=0 – полюс IV порядка;
3) z=0 – полюс III порядка;
184Определить характер особых точек:  =
= 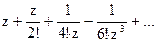
1) z=0 – существенно особая точка;
2) z=0 – простой полюс;
3) z=0 – полюс III порядка.
185Определить характер особых точек: 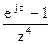 =
= 
1) z=0 – полюс I порядка;
2) z=0 – полюс IV порядка;
3) z=0 – полюс III порядка.
186Определить характер особых точек: 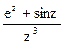 =
= 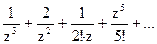
1) z=0 – полюс III порядка;
2) z=0 – полюс II порядка;
3) z=0 – полюс I порядка.
187Определить характер особых точек:
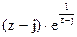 =
= 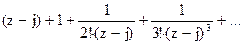
1) z=j – существенно особая точка;
2) z= –j – существенно особая точка;
3) z=j – простой полюс.
188Определить характер особых точек: 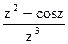 =
= 
1) z=0 – полюс I порядка;
2) z=0 – полюс III порядка;
3) z=0 – существенно особая точка.
189Определить характер особых точек: 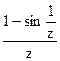 =
= 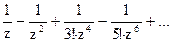
1) z=0 – устранимая особая точка;
2) z=0 – полюс I порядка;
3) z=0 – существенно особая точка.
190Определить характер особых точек: 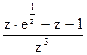 =
= 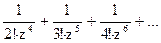
1) z=0 – существенно особая точка;
2) z=0 – полюс III порядка;
3) z=0 – полюс IV порядка.
191По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 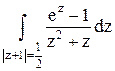 , res f(–1)=1–e–1
, res f(–1)=1–e–1
1) 2π j+1–e–1;
2) 1–e–1;
3) 2π j(1– 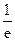 ).
).
192По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 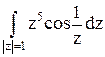 , res f(0)=
, res f(0)= 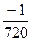
1) 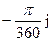 ;
;
2) 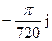 ;
;
3) 2π j– 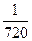 .
.
193По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 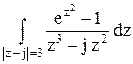 , res f(0)=0, res f(j)=1–e–1
, res f(0)=0, res f(j)=1–e–1
1) 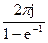 ;
;
2) 2π j(1– 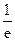 );
);
3) 1–e–1.
194По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 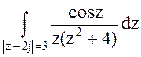 , res f(0)=
, res f(0)=  , res f(2j)= –
, res f(2j)= – 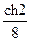
1) π j(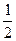 –
– 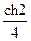 );
);
2) 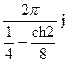 ;
;
3)  –
– 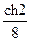 .
.
195По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 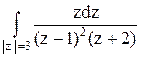 , res f(–2)= –
, res f(–2)= – 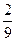 , res f(1)=
, res f(1)= 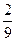
1) – 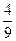 .
.
2) 2π j;
3) 0;
196По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 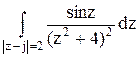 , res f(2j)=
, res f(2j)= 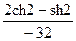
1) 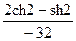 ;
;
2) 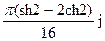 ;
;
3) 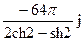 .
.
197По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 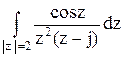 , res f(0)= 1, res f (j)= –ch1
, res f(0)= 1, res f (j)= –ch1
1) (2π –2π ·ch1)·j;
2) 1–ch1;
3) –2π ·ch1·j.
198По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 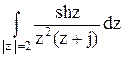 , res f(–j)= –jsin1, res f (0)= –j
, res f(–j)= –jsin1, res f (0)= –j
1) j·(–sin1–1);
2) –j·(sin1+1);
3) 2π ·sin1+2π.
199По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов: 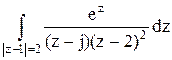 , res f(j)=
, res f(j)= 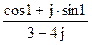 ,
,
res f (0)= 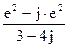
1) 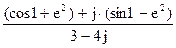 ;
;
2) 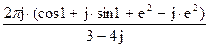 ;
;
3) 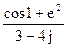 +j
+j  .
.
200По основной теореме о вычетах вычислить интеграл, если заданы значения вычетов:  , res f(1)=
, res f(1)= 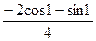
1)  ;
;
2) 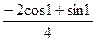 ;
;
3) 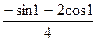 .
.