Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средние показатели в рядах динамики
|
|
Обобщенной характеристикой ряда динамики служат средние показатели:
· средний уровень ряда;
· средний абсолютный прирост;
· средний темп роста и прироста.
Для разных видов рядов динамики средний уровень рассчитывается неодинаково:
а) в интервальном ряду абсолютных величин с равными периодами (интервалами) – как средняя арифметическая простая из уровней ряда:
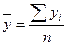 , (13)
, (13)
где 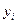 - отдельные уровни ряда;
- отдельные уровни ряда;
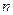 - число уровней;
- число уровней;
б) в итервальном ряду с неравными интервалами – как средняя арифметическая взвешенная:
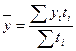 , (14)
, (14)
где 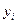 - уровни, сохраняющиеся неизменными в течение времени
- уровни, сохраняющиеся неизменными в течение времени 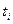 .
.
Пример. За март в списочном составе работников организации произошли следующие изменения, человек: состояло по списку на 01.03. – 540; выбыло 05.03. – 35; зачислено с 12.03 – 5; зачислено с 26.03 – 2. Определить среднесписочную численность работников организации за март месяц.
Решение. Построим расчетную таблицу:
| Календарные периоды марта | Число работников (y) | Длина периода, дней (t) | Число человеко-дней (yt) |
| 01-04 | |||
| 05-11 | |||
| 12-25 | |||
| 26-31 | |||
| итого | - |
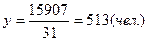 ;
;
в) в моментном ряду с равноотстоящими уровнями – как средняя хронологическая простая: 
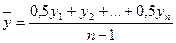 ; (15)
; (15)
г) в моментном ряду с неравноотстоящими уровнями – как средняя хронологическая взвешенная:
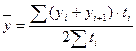 (16)
(16)
2. Средний абсолютный прирост (изменение) уровней рассчитывается как средняя арифметическая простая из отдельных цепных приростов, т.е.
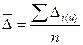 , (17)
, (17)
где 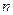 - число цепных приростов.
- число цепных приростов.
Он может быть также рассчитан на основе данных об абсолютном приросте за весь рассматриваемый период, т.е. через накопленный базисный абсолютный прирост:
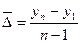 , (18)
, (18)
где 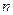 - число уровней ряда.
- число уровней ряда.
3. Средний коэффициент (темп) роста (снижения) исчисляется как средняя геометрическая из цепных темпов роста, т.е. рассчитанных в каждый период по отношению к предыдущему:
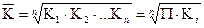 , (19)
, (19)
или иначе: 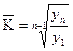 (20)
(20)
Средний темп роста:
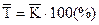 (21)
(21)
Пример. Объем произведенной продукции на предприятии (в сопоставимых ценах) характеризуется следующими данными:
| № п/п | Показатели | Единица измерения | ||||
| Объем произведенной продукции | млн. руб. | 35, 4 | 40, 6 | 44, 8 | 48, 2 | |
| Расчетные показатели | ||||||
| 1. | Абсолютный прирост: а) базисный; б) цепной | млн. руб. млн. руб. | - - | 5, 2 5, 2 | 9, 4 4, 2 | 12, 8 3, 4 |
| 2. | Темп роста: а) базисный; б) цепной | % % | - - | 114, 7 114, 7 | 126, 6 110, 3 | 136, 2 107, 6 |
| 3. | Темп прироста: а) базисный; б) цепной | % % | - - | 14, 7 14, 7 | 26, 6 10, 3 | 36, 2 7, 6 |
| 4. | Абсолютное значение 1% прироста | тыс. руб. | - |
5.Средний уровень ряда: 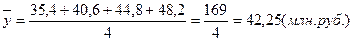
6. Средний абсолютный прирост:
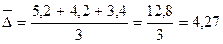
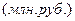
или 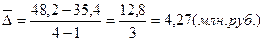

7. Среднегодовой коэффициент (темп) роста:
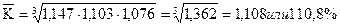
8. Среднегодовой темп прироста: