Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Г. Пааше и Э. Ласпейреса, их практическое применение
|
|
Статистические индексы (собственно индексы) строятся с учетом двух правил: взвешивания и элиминирования.
Взвешивание состоит в том, что индексируемый показатель умножают на другой, связанный с ним показатель, называемый весами индекса. Цель приема состоит в том, чтобы несоизмеримые явления (например, разнородные товары, измеряемые в кг, л., шт. или цены за 1кг, 1л, 1 шт.) привести к единству и получить сравнимые показатели, которые можно суммировать. Взвешивание позволяет рассматривать индексируемый показатель не изолированно, а во взаимосвязи с другими показателями.
Элиминирование – устранение влияния весов путем фиксирования их в числителе и знаменателе формулы индекса на уровне одного и того же периода.
Так, если товары, проданные в двух периодах, оценить по одним и тем же, например, базисным ценам (p0), то индекс отразит изменение только одного фактора – индексируемого показателя – q:
(6)
- общий индекс физического объема произведенной (реализованной) продукции.
Если же в формуле индекса предусмотреть лишь изменение цен (р), а количество товаров (q) зафиксировать в числителе и знаменателе на одном и том же уровне, то индекс будет характеризовать только изменение цен (т.е. индексируемого показателя), так как изменение весов (q) будет устранено (элиминировано), благодаря их фиксированию:
· либо на уровне отчетного периода
(7)
- общий индекс цен Г.Пааше (по имени немецкого экономиста, впервые предложившего его в 1874г.);
· либо на уровне базисного периода
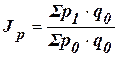(8)
- общий индекс цен Э. Ласпейреса (по имени немецкого экономиста, предложившего его в 1864г.).
Значения индексов цен Пааше и Ласпейреса не совпадают (первый всегда меньше), что связано с их различным экономическим содержанием.
Индекс цен Пааше показывает, насколько товары в текущем периоде стали дороже (дешевле), чем в базисном. Индекс цен Ласпейреса дает ответ на вопрос, насколько товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде.
Общий индекс цен Пааше используется, когда нужно определить, сколько денег население переплатило за продукцию, купленную в текущем периоде в связи с ростом цен.
Общий индекс цен Ласпейреса используется для расчета ИПЦ и показывает, насколько дороже стала «потребительская корзина» прошлого года в текущем периоде. Он отражает уровень инфляции на потребительском рынке, а, следовательно, показывает удорожание стоимости жизни или снижение уровня жизни населения в связи с ростом цен.
Для разноименных товаров (услуг) вычисляют индексы по методикам:
Эджворта – Маршалла
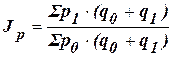(9)
Фишера (так называемая “идеальная” формула)
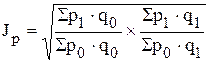(10)
По аналогии можно записать агрегатные индексы для многих других показателей:
· агрегатный индекс себестоимости –
Iz =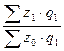 
(11)
· общий индекс урожайности в агрегатной форме –
Iy =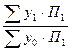 
, (12)
где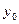 
и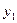 
– урожайность отдельных культур (например, для зерновых культур – это урожайность пшеницы, ржи, ячменя и др.) в базисном и отчетном периодах;
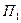– посевная площадь под отдельными (зерновыми) культурами в текущем периоде;
· сводный индекс производительности труда в агрегатной форме Iw =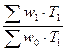 
, (13)
где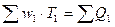 
= – фактический объем продукции, произведенной в отчетном периоде;
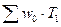– условная величина, показывающая, каким был бы выпуск продукции в отчетном периоде при численности работников отчетного периода, но базисной выработке.
· агрегатный индекс производительности труда, выраженной обратной величиной – трудоемкостью (t) –
Iw =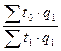 
, (14)
где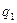 
– выпуск продукции отдельных видов в натуральном выражении в отчетном периоде;
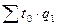– условные затраты времени на выпуск продукции отчетного периода при базисной трудоемкости;
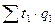– затраты времени на весь объем продукции в отчетном периоде.
Пример. Имеются следующие данные о продаже товаров рыночной торговлей города:
| Товары | Ед. измер. | Цены, руб. | Количество продаж | ||
| База | Отчет | База | Отчет | ||
| А | л. | 1 500 | 1 100 | ||
| В | кг. | 2, 5 | 3 000 | 5 000 | |
| С | шт. | 20 000 | 30 000 |
Проанализируем данные таблицы с помощью индексов.
1. Как изменились цены в отчетном периоде по сравнению с базисным по каждому товару в отдельности.
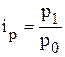- индивидуальный индекс цен
; 
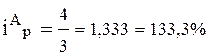
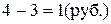
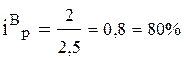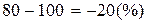; 2 – 2, 5 = - 0, 5 (руб)
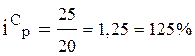
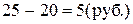
Вывод: По товару А цены повысились на 33, 3%, или на 1руб. за 1 л., по товару В – снизились на 20% или на 0, 5 руб. за 1 кг., а по товару С повысились на 25% или на 5 руб. за 1 шт.
2. Как изменилось количество проданных товаров в отчетном периоде по сравнению с базисным по каждому товару отдельно?
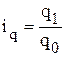- индивидуальный индекс физического объема реализации
; 
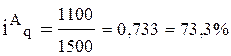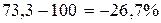; 1100– 1500 = - 400 (л)
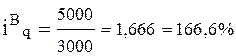; 5000 – 3000 = 2000 (кг)
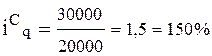; 30 000 – 20 000 = 10 000 (шт.)
Вывод: В отчетном периоде по сравнению с базисным количество проданного товара А снизилось на 26, 7% или на 400 л., по товару В физический объем реализации увеличился на 66, 6 % или на 2000 кг, а по товару С – на 50% (в 1, 5 раза) или на 10 000 шт.
3. Как изменились цены по трем товарам вместе?
Используя формулу (7), определим общий индекс цен:
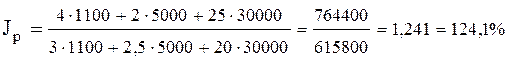
Переплата составила D p× q (р) = 764400 – 615800 = 148600 (руб.)
Вывод: По трем товарам вместе цены выросли на 24, 1%, что вызвало переплату в сумме 148600 руб.
4. Как изменилось общее кол-во проданных товаров в отчетном периоде по сравнению с базисным?
Используя формулу (6), определим общий индекс физического объема продаж:
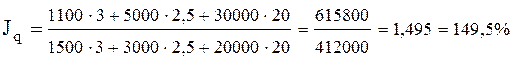
D p× q (q) = 615800 – 412000 = 203800 (руб.)
Вывод: В отчетном периоде по сравнению с базисным, количество всех проданных товаров увеличилось на 49, 5 % или на 203800 руб.
5. Как изменилась стоимость всех проданных товаров в отчетном периоде по сравнению с базисным?
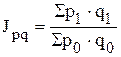- общий индекс товарооборота
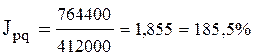
D p× q общ. = 764400 – 412000 = 352400 (руб.)
Вывод: Стоимость всех проданных товаров в отчетном периоде по сравнению с базисным выросла на 85, 5% или на 352400 руб.
Взаимосвязь исчисленных индексов:
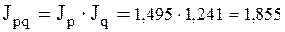
Взаимосвязь абсолютных пофакторных изменений:
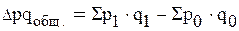
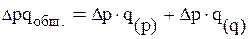
Проверим эту взаимосвязь:
148 600 + 203 800 = 352 400 (руб.)