Методы выявления основной тенденции развития в рядах динамики. Прогнозирование экономических показателей на основе динамических рядов

Уровни ряда динамики формируются под влиянием взаимодействия многих факторов, одни из которых, будучи основными, определяют закономерность, тенденцию развития, другие – случайные – вызывают колебания уровней. Можно сказать, что динамика ряда включает три компоненты:

• долговременное движение (так называемый тренд);
• кратковременное систематическое движение (например, сезонные колебания);
• несистематическое случайное движение, вызывающее колебания уровней относительно тренда.

Изучая ряды динамики, исследователи пытаются разделить эти компоненты и выявить основную закономерность развития явления или общую тенденцию в изменении уровней рядов, освобожденную от действия случайных факторов. Выявление основной тенденции развития (тренда) называется в статистике выравниванием временного ряда, а методы обработки рядов - методами сглаживания или выравнивания рядов динамики. Наиболее часто применяются следующие методы: укрупнения интервалов, скользящей средней и аналитического выравнивания.

1. Простейший метод сглаживания уровней ряда – укрупнение интервалов, смысл которого заключается в преобразовании первоначального ряда динамики и замене его другим, уровни которого относятся к большим по продолжительности периодам времени (квартальными вместо месячных). Вновь образованный ряд может содержать либо абсолютные величины за укрупненные промежутки времени, получаемые суммированием уровней первоначального ряда, либо средние величины.

В результате такого преобразования отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более отчетливо обнаруживается действие основных факторов изменения уровней (общая тенденция).

2. Метод скользящей средней. Для определения скользящей средней формируют укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получают, постепенно сдвигаясь от начального уровня на один уровень. Тогда первый интервал будет включать уровни у₁, у₂, …, у_m; второй - у₂, у₃, …, у_m+1 и т.д. Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяют суммы значений уровней, на основе которых рассчитывают скользящие средние.

3. Аналитическое выравнивание ряда динамики используется тогда, когда хотят дать количественную модель, выражающую общую тенденцию изменений уровней во времени.

В этом случае фактические (эмпирические) уровни 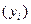заменяются теоретическими уровнями 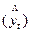, вычисленными по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: .

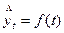В аналитическом выравнивании наиболее часто используются следующие простейшие функции:

• линейная 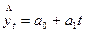; (22)
• показательная 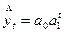; (23)
• гиперболическая 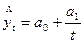; (24)
• парабола 2-го (или более высокого) порядка: 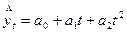. (25)

Здесь 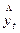- теоретические (выравненные) уровни (читается: «игрек, выравненный по 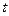»), 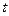– условное обозначение времени (1, 2, 3, …), 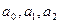- параметры аналитической функции.

Выбор той или иной функции для выравнивания ряда динамики осуществляется, как правило, на основании графического изображения эмпирических данных, дополняемого содержательным анализом особенностей развития исследуемого показателя (явления) и специфики разных функций, их возможности отразить те или иные нюансы развития. Определенную вспомогательную роль при выборе аналитической функции играют также механические приемы сглаживания (укрупнение интервала и метод скользящей средней). Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель (уравнение) для аналитического выравнивания.

Кроме того, в результате многолетнего опыта использования аналитического выравнивания рядов динамики наработаны некоторые правила или, вернее, условия использования перечисленных простых уравнений, которыми полезно руководствоваться при выборе функции.

1. Так, выравнивание по прямой линии (линейной функции) эффективно для рядов, уровни которых изменяются примерно в арифметической прогрессии, т.е. когда первые разности уровней (абсолютные приросты) более или менее постоянны.

2. Если вторые разности уровней (ускорения) более или менее постоянны, то такое развитие хорошо описывается параболой 2-го порядка. Парабола 2-го порядка отражает развитие с ускоренным или замедленным изменением уровней ряда. Если постоянны 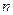-е разности уровней, можно использовать параболу 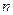- го порядка, позволяющую «улавливать» перегибы, изломы в кривой, смену направлений изменения уровней.

3. Если при последовательном расположении t (меняющемся в арифметической прогрессии значения уровней меняются в геометрической прогрессии, т.е. цепные коэффициенты роста примерно постоянны, то такое развитие можно отразить показательной функцией.

4. Если обнаружено замедленное снижение уровней ряда, которые по логике не могут снизиться до нуля, для описания характера тренды выбирают гиперболу и т. д.

Если по тем или иным причинам уровни эмпирического ряда трудно математически описать одной функцией, следует разбить исследуемый период на отдельные части и затем выровнять каждую часть по соответствующей кривой.

Чтобы решить вопрос о том, использование какой кривой дает лучший результат, обычно сопоставляют суммы квадратов отклонений эмпирических уровней от теоретических, рассчитанных по разным функциям, т. е. 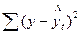. Та функция, при которой эта сумма квадратов меньше, считается более адекватной, приемлемой.

Аналитическое выравнивание ряда динамики по прямой производится на основе аналитического уравнения вида .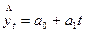

Параметры 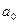и 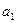прямой рассчитываются по методу наименьших квадратов. Система нормальных уравнений в данном случае имеет вид:

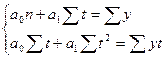(26)

Система нормальных уравнений и, соответственно, расчет параметров 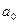и 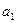упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно -1, -2, -3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д.

При четном числе уровней два серединных момента (периода) времени обозначают -1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 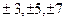и т.д.

При таком порядке отсчета времени (от середины ряда) 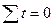, поэтому система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:

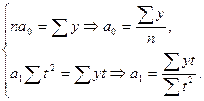(27)

Рассмотрим аналитическое выравнивание по прямой на примере.

Пример. Известны следующие данные о выдаче краткосрочных кредитов:

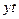
Месяцы	Краткосрочные кредиты, тыс.руб. (y)	Условное обозначение периодов (t)			Выравненный ряд динамики
январь		-3		-330	105, 8
февраль		-2		-230	113, 2
март		-1		-112	120, 6
апрель
май					135, 4
июнь					142, 8
июль					150, 2
итого		-

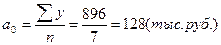
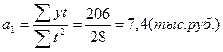
Уравнение прямой примет вид:

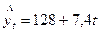
По уравнению исчислим уровни выравненного ряда динамики:

для января при ;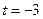

для февраля при 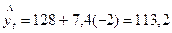и т. д.

Правильность расчета уровней выравненного ряда динамики может быть проверена следующим образом: сумма фактических значений должна совпадать с суммой вычисленных уровней выравненного ряда, т.е. 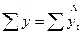. В нашем примере 896=896.

Изучая и анализируя ряды динамики, исследователи всегда стремились на основе выявленных особенностей изменения явлений в прошлом предугадать поведение рядов в будущем, т.е. пытались строить различные прогнозы путем экстраполяции – продления в будущее тенденции, наблюдавшейся в прошлом.

Рассмотрим некоторые простейшие приемы экстраполяции рядов динамики.

1. Если при анализе ряда динамики обнаруживается, что абсолютные приросты уровней примерно постоянны, можно рассчитать средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд;

2. Если за исследуемый ряд лет (или другие периоды) годовые коэффициенты роста остаются более-менее постоянными, можно рассчитать средний коэффициент роста и умножить последний уровень ряда на средний коэффициент роста в степени, соответствующей периоду экстраполяции;

3. Учитывая, что между изменениями нескольких показателей существует зависимость, можно экстраполировать один ряд динамики на основе сведений об изменении второго ряда, связанного с ним. Так, определив, какой будет численность детей через t лет (по таблицам смертности), можно определить ожидаемое потребление детских товаров.

4. Можно экстраполировать ряды на основе выравнивания их по определенной аналитической формуле. Зная уравнение для теоретических уровней и подставляя в него значение t за пределами исследуемого ряда, можно рассчитать для данных t вероятностные уровни .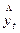

В нашем примере, экстраполируя при t = 4, определим уровень августа:

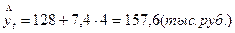
Возможность экстраполяции обеспечивается двумя обстоятельствами:

• общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;
• тенденция развития явления характеризуется тем или иным аналитическим уравнением. Правильность его выбора обеспечивает надежность прогноза.

Результаты экстраполяции следует подвергать математической обработке, определяя так называемые доверительные интервалы прогноза.

Экстраполяцию следует рассматривать не как завершающую стадию прогнозирования, а лишь как предварительный этап в разработке прогноза. Для составления прогноза должна быть привлечена дополнительная информация, не содержащаяся в самом динамическом ряду.

Аналитическое выравнивание ряда динамики позволяет также по имеющимся данным за определенный период рассчитывать некоторые недостающие значения внутри этого периода (интерполяция) или в начале динамического ряда (ретрополяция).