Доказательство теоремы Пифагора

Пусть треугольник 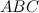- прямоугольный треугольник с прямым углом 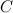(рис. 2).

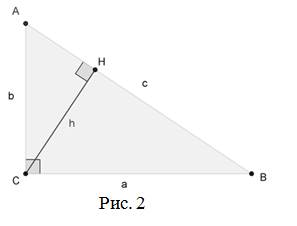
Проведём высоту из вершины 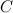на гипотенузу 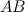, основание высоты обозначим как .

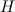Прямоугольный треугольник 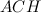подобен треугольнику 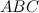по двум углам (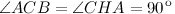, 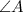- общий). Аналогично, треугольник 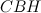подобен .

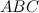Введя обозначения

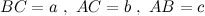
из подобия треугольников получаем, что

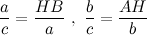
Отсюда имеем, что

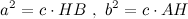
Сложив полученные равенства, получаем

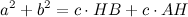
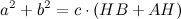
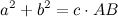
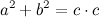
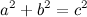
Что и требовалось доказать.

Геометрическая формулировка теоремы Пифагора

Теорема

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 2):

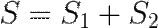
Примеры решения задач

Пример

Задание. Задан прямоугольный треугольник 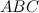, катеты которого равны 6 см и 8 см. Найти гипотенузу этого треугольника.

Решение. Согласно условию катеты 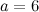см, 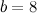см. Тогда, согласно теореме Пифагора, квадрат гипотенузы

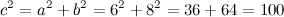
Отсюда получаем, что искомая гипотенуза

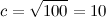(см)

Ответ. 10 см

Пример

Задание. Найти площадь прямоугольного треугольника, если известно, что один из его катетов на 5 см больше другого, а гипотенуза равна 25 см.

Решение. Пусть см - длина меньшего катета, тогда 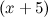см - длина большего. Тогда согласно теореме Пифагора имеем:

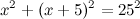
Раскрываем скобки, сводим подобные и решаем полученное квадратное уравнение:

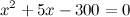
Согласно теореме Виета, получаем, что

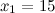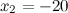(см), (см)

Значение 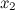не удовлетворяет условию задачи, а значит, меньший катет равен 15 см, а больший - 20 см.

Площадь прямоугольного треугольника равна полупроизведению длин его катетов, то есть

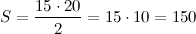(см²)

Ответ. 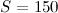(см²)

Вопрос 8.

I. Признак подобия треугольников по двум углам.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

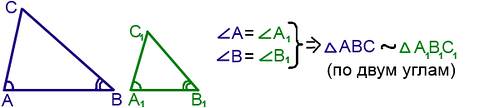
II. Признак подобия треугольников по двум сторонам и углу между ними.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

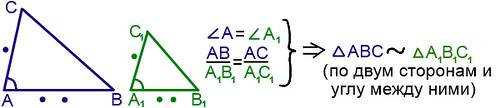
III. Признак подобия треугольников по трем сторонам.

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

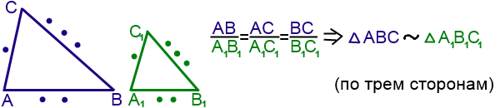
Признак подобия прямоугольных треугольников

Для подобия прямоугольных треугольников достаточно, чтобы у них было по одному острому углу.

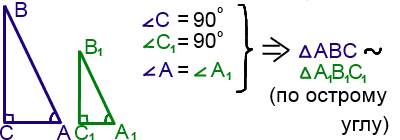
Из подобия треугольников следует равенство соответствующих углов и пропорциональность сторон:

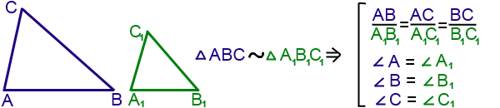
Периметры подобных треугольников пропорциональны:

k — коэффициент подобия.

Все линейные размеры подобных треугольников также пропорциональны, то есть отношение соответствующих биссектрис, высот, медиан также равно k.

Углы между соответствующими линиями подобных треугольников равны.

Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:

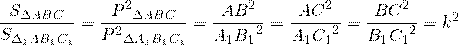
Вопрос 9

I. Признак подобия треугольников по двум углам.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

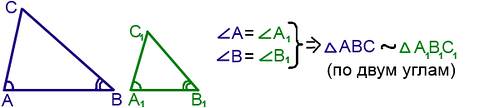
II. Признак подобия треугольников по двум сторонам и углу между ними.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.

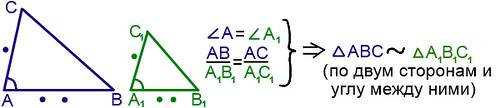
III. Признак подобия треугольников по трем сторонам.

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

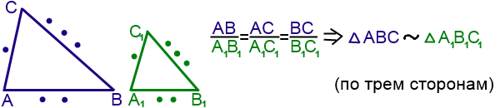
Признак подобия прямоугольных треугольников

Для подобия прямоугольных треугольников достаточно, чтобы у них было по одному острому углу.

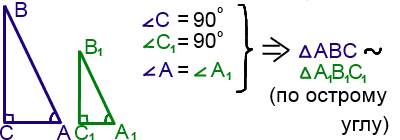
Из подобия треугольников следует равенство соответствующих углов и пропорциональность сторон:

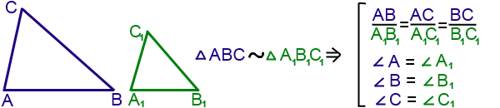
Периметры подобных треугольников пропорциональны:

k — коэффициент подобия.

Все линейные размеры подобных треугольников также пропорциональны, то есть отношение соответствующих биссектрис, высот, медиан также равно k.

Углы между соответствующими линиями подобных треугольников равны.

Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:

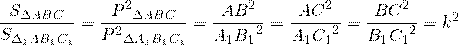
Вопрос 10

Окружностью с центром в точке О и радиусом R называют множество всех точек плоскости, удаленных от точки О на расстояние R.

Обратим внимание на то, что окружностью называют именно множество всех точек, удовлетворяющих описанному условию. Рассмотрим пример:

Точки A, B, C, D квадрата равноудалены от точки Е, но они не являются окружностью (рис. 1).

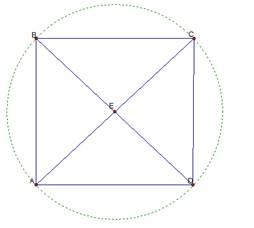
Рис. 1. Иллюстрация к примеру

В данном случае фигура является окружностью, так как это все множество точек, равноудаленных от центра.

Если соединить любые две точки окружности – получаем хорду. Хорда, проходящая через центр, называется диаметром.

MB – хорда; АВ – диаметр; MnB – дуга, она стягивается хордой МВ;

Угол называется центральным.

Точка О – центр окружности.

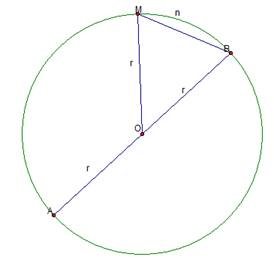
Рис. 2. Иллюстрация к примеру

Таким образом, мы вспомнили, что такое окружность и основные ее элементы. Теперь перейдем к рассмотрению взаимного расположения окружности и прямой.

Задана окружность с центром О и радиусом r. Прямая Р, расстояние от центра до прямой, то есть перпендикуляр ОМ, равна d.

Считаем, что точка О не лежит на прямой Р.

Взаимное расположение прямой и окружности, случай с двумя общими точками

По заданным окружности и прямой нам необходимо найти число общих точек.

Случай 1 – расстояние от центра окружности до прямой меньше радиуса окружности:

В первом случае, когда расстояние d меньше радиуса окружности r, точка М лежит внутри окружности. От этой точки мы отложим два отрезка – МА и МВ, длинна которых будет 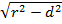. Значения r и d нам известны, d меньше r, значит, выражение 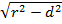существует и точки А и В существуют. Эти две точки лежат на прямой по построению. Проверим, лежат ли они на окружности. Вычислим по теореме Пифагора расстояние ОА и ОВ:

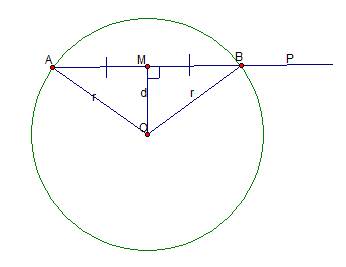
Рис. 3. Иллюстрация к случаю 1

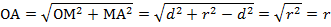
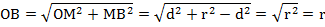
Расстояние от центра до двух точек равно радиусу окружности, таким образом, мы доказали, что точки А и В принадлежат окружности.

Итак, точки А и В принадлежат прямой по построению, принадлежат окружности по доказанному – окружность и прямая имеют две общих точки. Докажем, что других точек нет (рис. 4).

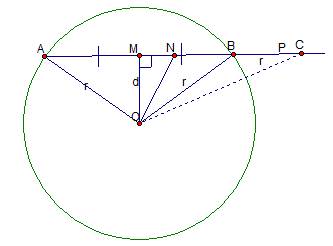
Рис. 4. Иллюстрация к доказательству

Для этого возьмем на прямой произвольную точку С и предположим, что она лежит на окружности – расстояние ОС=r. В таком случае треугольник 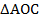равнобедренный и его медиана ON, которая не совпадает с отрезком ОМ, является высотой. Мы получили противоречие: из точки О опущено два перпендикуляра на прямую.

Таким образом, на прямой Р нет других общих точек с окружностью. Мы доказали, что в случае, когда расстояние d меньше радиуса окружности r, прямая и окружность имеют только две общие точки.

Взаимное расположение прямой и окружности, случай с одной общей точкой

Случай второй – расстояние от центра окружности до прямой равно радиусу окружности (рис. 5):

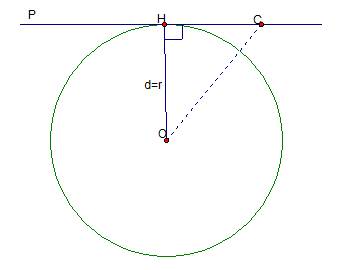
Рис. 5. Иллюстрация к случаю 2

Напомним, что расстояние от точки до прямой – это длина перпендикуляра, в данном случае ОН – перпендикуляр. Так как, по условию, длина ОН равна радиусу окружности, то точка Н принадлежит окружности, таким образом, точка Н общая для прямой и окружности.

Докажем что других общих точек нет. От противного: предположим, что точка С на прямой принадлежит окружности. В таком случае, расстояние ОС равно r, и тогда ОС равно ОН. Но в прямоугольном треугольнике 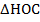гипотенуза ОС больше катета ОН. Получили противоречие. Таким образом, предположение неверно и нет никакой точки кроме Н, общей для прямой и окружности. Мы доказали, что в данном случае общая точка единственная.

Взаимное расположение прямой и окружности, случай, когда нет общих точек

Случай 3 – расстояние от центра окружности до прямой больше радиуса окружности:

Расстояние от точки до прямой – длина перпендикуляра. Проводим из точки О перпендикуляр к прямой Р, получаем точку Н, которая не лежит на окружности, так как ОН по условию больше радиуса окружности. Докажем, что любая другая точка прямой не лежит на окружности. Это хорошо видно из прямоугольного треугольника 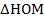, гипотенуза ОМ которого больше катета ОН, а значит, больше радиуса окружности, таким образом, точка М не принадлежит окружности, как и любая другая точка на прямой. Мы доказали, что в данном случае окружность и прямая не имеют общих точек (рис. 6).

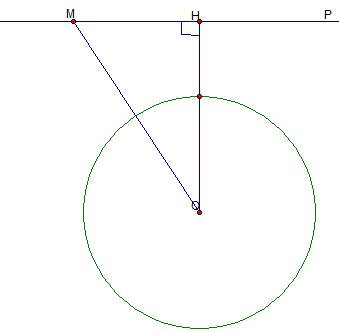
Рис. 6. Иллюстрация к случаю 3

Теоремы о диаметре и хорде

Рассмотрим теорему. Предположим, что прямая АВ имеет две общих точки с окружностью (рис. 7).

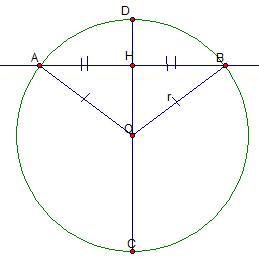
Рис. 7. Иллюстрация к теореме

Имеем хорду АВ. Точка Н, по условию, – середина хорды АВ и лежит на диаметре СD.

Требуется доказать, что в таком случае диметр перпендикулярен хорде.

Доказательство:

Рассмотрим равнобедренный треугольник 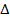ОАВ, он равнобедренный, так как .

Точка Н, по условию, – середина хорды, значит середина медианы АВ равнобедренного треугольника. Мы знаем, что медиана равнобедренного треугольника перпендикулярна его основанию, значит, является высотой: 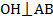, отсюда 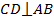, таким образом, доказано, что диаметр, проходящий через середину хорды, перпендикулярен ей.

Справедлива и обратная теорема: если диаметр перпендикулярен хорде, то он проходит через ее середину.

Задана окружность с центром О, ее диаметр СD и хорда АВ. Известно, что диаметр перпендикулярен хорде, нужно доказать, что он проходит через ее середину (рис. 8).

Рис. 8. Иллюстрация к теореме

Доказательство:

Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как . ОН, по условию, – высота треугольника, так как диаметр перпендикулярен хорде. Высота в равнобедренном треугольнике одновременно является медианой, таким образом, АН=НВ, значит, точка Н является серединой хорды АВ, значит, доказано, что диаметр, перпендикулярный хорде, проходит через ее середину.

Прямую и обратную теорему можно обобщить следующим образом.

Теорема:

Диаметр перпендикулярен хорде тогда и только тогда, когда он проходит через ее середину.

Выводы по уроку

Итак, мы рассмотрели все случаи взаимного расположения прямой и окружности. На следующем уроке мы рассмотрим касательную к окружности.

Вопрос 11.

редней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

Дано: DE — средняя линия треугольника ABC.



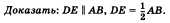
Доказательство. Проведем через точку D прямую, параллельную стороне АВ. По теореме Фалеса она пересекает отрезок АС в его середине, т. е. содержит среднюю линию DE. Значит, средняя линия DE параллельна стороне АВ (рис. 53).

Проведем теперь среднюю линию DF. Она параллельна стороне АС. Четырехугольник AEDF — параллелограмм. По свойству параллелограмма ED = — AF, а так как AF = FB по теореме Фалеса, то ED = АВ. Теорема доказана.

вопрос 12.

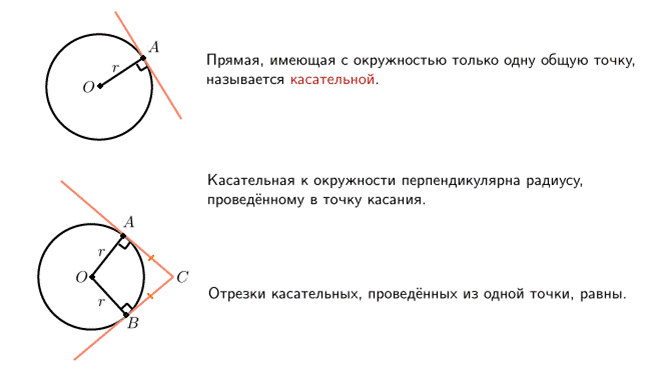
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.

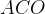. Угол равен 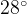, где 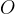— центр окружности. Его сторона 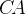касается окружности. Найдите величину меньшей дуги 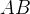окружности, заключенной внутри этого угла. Ответ дайте в градусах.

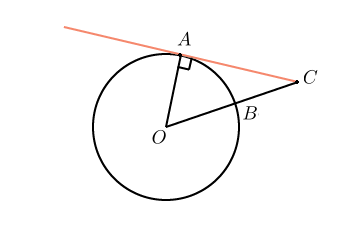
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол 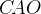— прямой. Из треугольника 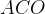получим, что угол 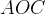равен 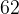градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги 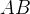— тоже 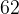градуса.

Ответ: .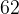

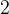. Найдите угол 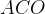, если его сторона 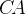касается окружности, 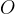— центр окружности, а большая дуга 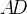окружности, заключенная внутри этого угла, равна 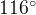. Ответ дайте в градусах.

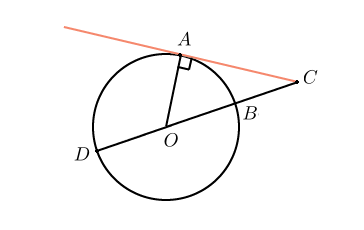
Это чуть более сложная задача. Центральный угол 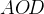опирается на дугу 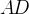, следовательно, он равен 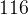градусов. Тогда угол 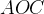равен 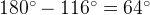. Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол 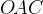— прямой. Тогда угол 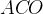равен .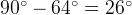

Ответ: .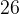

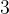. Хорда 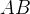стягивает дугу окружности в 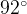. Найдите угол между этой хордой и касательной к окружности, проведенной через точку . Ответ дайте в градусах.

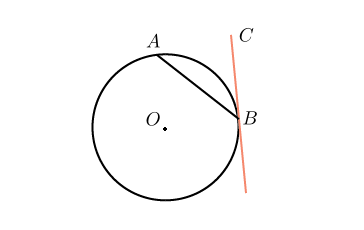
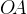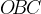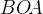Проведем радиус в точку касания, а также радиус . Угол равен . Треугольник — равнобедренный. Нетрудно найти, что угол 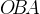равен 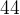градуса, и тогда угол 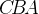равен 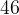градусов, то есть половине угловой величины дуги .

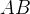Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

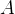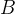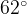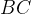. Через концы , дуги окружности в проведены касательные и . Найдите угол 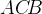. Ответ дайте в градусах.

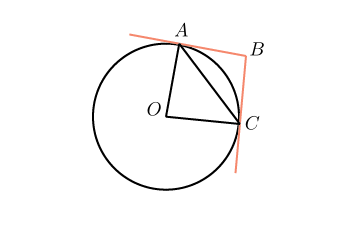
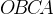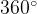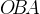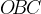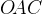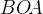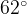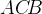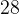Рассмотрите четырехугольник . Сумма углов любого выпуклого четырехугольника равна . Углы и и — прямые, угол равен , значит, угол равен градусов.

Ответ: .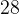

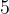. К окружности, вписанной в треугольник 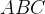, проведены три касательные. Периметры отсеченных треугольников равны 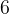, , 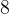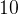. Найдите периметр данного треугольника.

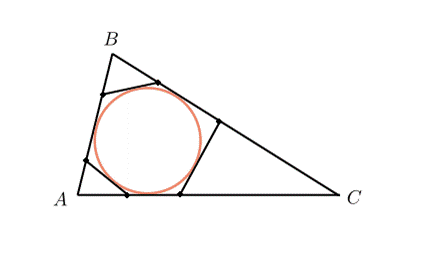
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника 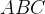складывается из периметров отсеченных треугольников.

Ответ: .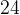

Вопрос 13.

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

[П] Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Дано: ABC — вписанный, О — центр окружности.





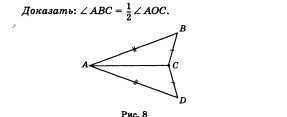
Доказательство. Рассмотрим сначала частный случай, когда одна из сторон угла проходит через центр окружности (рис. 9, а).

Треугольник АОВ равнобедренный, так как у него стороны ОА и ОВ равны как радиусы. Поэтому углы А и В треугольника равны. А так как их сумма равна внешнему углу треугольника при вершине О, то угол В треугольника равен половине угла АОС, что и требовалось доказать.

Общий случай сводится к рассмотренному частному случаю проведением вспомогательного диаметра BD (рис. 9, б, в).

В случае, представленном на рисунке 9, б,



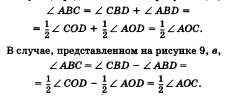
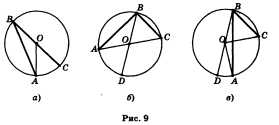
[А] Вписанный угол измеряется половиной дуги, на которую он опирается.

Дано: ABC — вписанный, О — центр окружности, АС соответствует ABC (рис. 10).

Вопрос 14.

При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.

угол BAD = углу BCD = 1/2 BmD

=> треуг. APD = треуг. CPD (по двум углам)

PD/PB = AP/CP. доказано.

Вопрос 15.

Биссектрисой (от лат. bi - " двойное", и sectio - " разрезание") угла называется луч, который исходит извершины угла и делить угол на две равные части (пополам) (рис. 1).

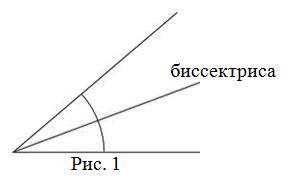
Мнемоническое правило: биссектриса это крыса, которая бегает по углам и делит угол пополам.

Пример

Задание. В угле 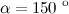проведена биссектриса. Чему равен каждый из полученных углов?

Решение. Так как по определению биссектриса делит угол на два равных, то полученные углы равны соответственно

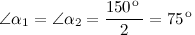
Ответ. 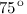и