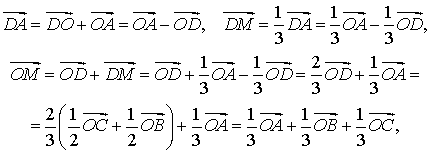Выводы по уроку

Итак, мы рассмотрели теорему о пересечении высот треугольника, на следующем уроке мы рассмотрим окружность, вписанную в треугольник.

Вопрос 18.

Теорема о центре окружности, вписанной в треугольник.

Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Дано: АВС — данный треугольник; О — центр вписанной в него окружности; D, Е и F — точки касания окружности со сторонами треугольника (рис. 27).

Доказать: О — точка пересечения биссектрис.

Доказательство. Прямоугольные треугольники AOD иАОЕ равны по гипотенузе и катету. У них гипотенуза ОА — общая, а катеты OD и ОЕ равны как радиусы. Из равенства треугольников следует равенство углов OAD и ОАЕ. А это значит, что точка О лежит на биссектрисе треугольника, проведенной из вершины А. Точно так же доказывается, что точка О лежит на двух биссектрисах треугольника.

[А] Теорема об окружности, вписанной в треугольник.

В любой треугольник можно вписать окружность.



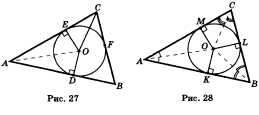
Дано: A ABC — данный треугольник, О — точка пересечения биссектрис, М, L и К — точки касания окружности со сторонами треугольника (рис. 28).

Доказать: О — центр окружности, вписанной в АВС.

Доказательство. Проведем из точки О перпендикуляры OK, OL и ОМ соответственно к сторонам АВ, ВС и СА (см. рис. 28). Так как точка О равноудалена от сторон треугольника ABC, то О К = OL = = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки K L M. Стороны треугольника ABC касаются этой окружности в точках К, L, М, так как они перпендикулярны к радиусам ОК, OL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник ABC. Теорема доказана.

Замечание. Отметим, что в треугольник можно вписать только одну окружность. В самом деле, допустим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают.

Вопрос 19.

еорема о центре окружности, описанной около треугольника.

Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.

Дано: АВС — данный треугольник; О — центр описанной около него окружности (рис. 30).

Доказать: О — точка пересечения серединных перпендикуляров.



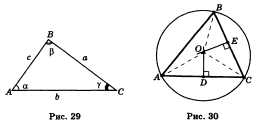
Доказательство. Треугольник АОС равнобедренный: у него стороны О А и ОС равны как радиусы. Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне АС и проходящей через ее середину. Точно так же доказывается, что центр окружности лежит на перпендикулярах к двум другим сторонам треугольника.

Замечание. Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.

[А] Теорема об окружности, описанной около треугольника.

Около любого треугольника можно описать окружность.

Дано: АВС — данный треугольник; О — точка пересечения серединных перпендикуляров (рис. 31).

Доказать: О — центр окружности, вписанной в АВС.

Доказательство. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, тоОА = OB — ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.

Замечание. Отметим, что около треугольника можно описать только одну окружность. В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой окружности равноудален от вершин треугольника и, значит, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают.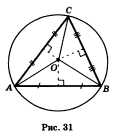

вопрос 20!

Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

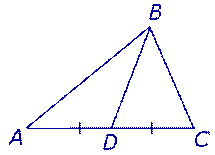
Рис.1

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD.

Утверждение 1. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).

Доказательство. Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

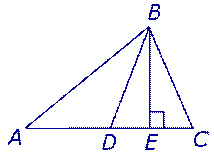
Рис.2

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

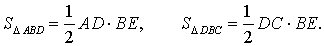
Поскольку отрезок BD является медианой, то

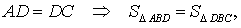
что и требовалось доказать.

Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2: 1, считая от вершины треугольника.

Доказательство. Рассмотрим две любых медианы треугольника, например, медианы AD и CE, и обозначим точку их пересечения буквой O (рис. 3).

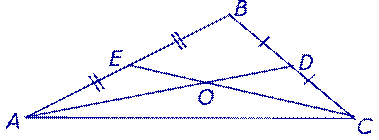
Рис.3

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

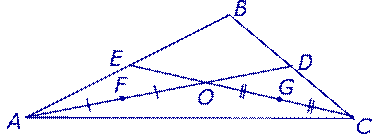
Рис.4

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

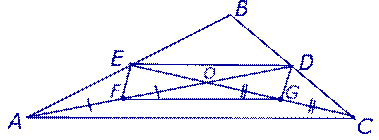
Рис.5

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC. Следовательно,

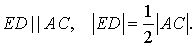
Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC. Следовательно,

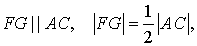
откуда вытекает, что стороны ED и FG четырёхугольника FEDG равны и параллельны.Следовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополам (рис.6).

Рис.6

Таким образом,

| FO | = | OD |, | GO | = | OE |.

Следовательно,

| AF | = | FO | = | OD |, | CG | = | GO | = | OE |.

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2: 1, считая от вершины треугольника.

Доказательство завершено.

Следствие. Все три медианы треугольника пересекаются в одной точке.

Доказательство. Рассмотрим медиану AD треугольника ABC и точку O, которая делит эту медиану в отношении 2: 1, считая от вершины A (рис.7).

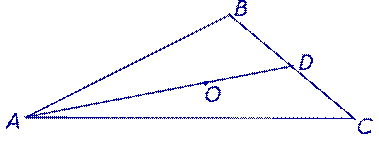
Рис.7

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение. Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

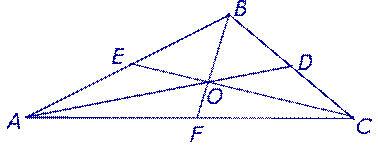
Рис.8

Доказательство. Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна 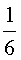площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

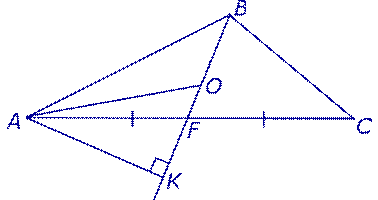
Рис.9

Тогда

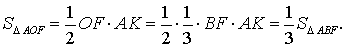
В силу утверждения 1,

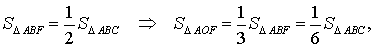
что и требовалось доказать.

Утверждение 4. Длина медианы треугольника (рис. 10) вычисляется по формуле:

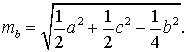
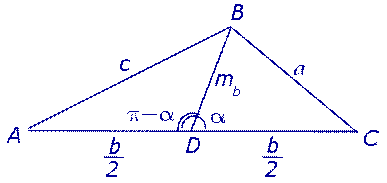
Рис.10

Доказательство. Воспользуемся теоремой косинусов, примененной к треугольникам DBC и ABD:

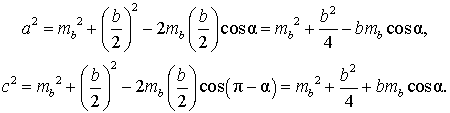
Складывая эти равенства, получим:

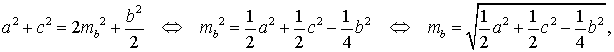
что и требовалось доказать.

Следствие. Длины медиан и длины сторон треугольника связаны формулой

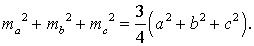
Доказательство. В силу утверждения 4 справедливы равенства:

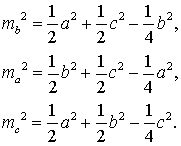
Складывая эти равенства, получим:

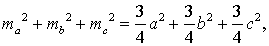
что и требовалось доказать.

Утверждение 5. В параллелограмме сумма квадратов диагоналей равна сумме квадратов сторон.

Доказательство. Рассмотрим рисунок 11.

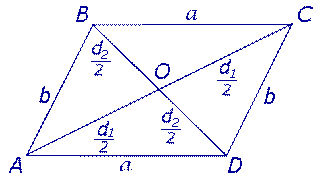
Рис.11

Поскольку AO – медиана треугольника ABD, а DO – медиана треугольника ADC, то, в силуутверждения 4, справедливы равенства:

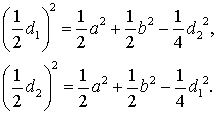
Следовательно,

d ₁² = 2 a ² + 2 b ² – d ₂²,

d ₂² = 2 a ² + 2 b ² – d ₁².

Складывая эти равенства, получим

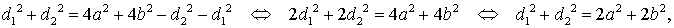
что и требовалось доказать.

Утверждение 6. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы (рис. 12).

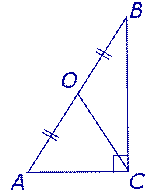
Рис.12

Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B (рис. 13).

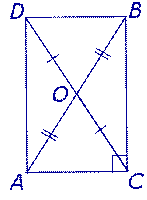
Рис.13

Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства:

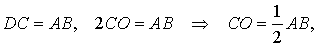
что и требовалось доказать.

Следствие. Середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности (рис. 14).

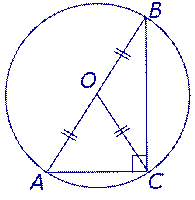
Рис.14

Утверждение 7. Рассмотрим в пространстве или на плоскости декартову систему координат с началом в точке O и произвольный треугольник ABC. Если обозначить буквой M точку пересечения медиан этого треугольника (рис.15), то будет справедливо равенство

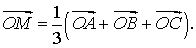
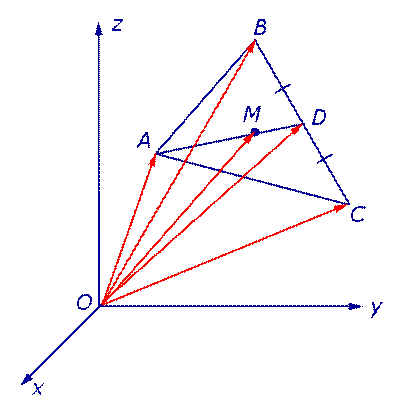
Рис.15

Доказательство. По свойствам векторов

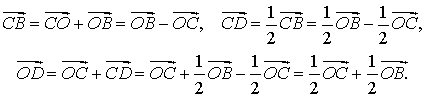
Далее получаем