Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

II) И обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

I)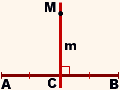

Дано:

AB- отрезок, C — середина AB,

m — серединный перпендикуляр к AB,

M∈ m.

Доказать: AM=BM.

Доказательство:

1. Если точка M совпадает с точкой C.

Так как AC=BC по условию, то и AM=BM.

2. Если точка M не совпадает с точкой C.

Рассмотрим треугольники ACM и BCM

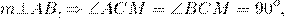
то есть треугольники ACM и BCM — прямоугольные.

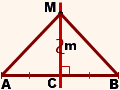
AC=BC (по условию), CM — общий катет.

Следовательно, ∆ ACM=∆ BCM (по двум катетам).

Из равенства треугольников следует равенство соответствующих сторон: AM=BM.

Что и требовалось доказать.

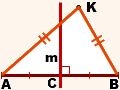II) Дано: AB — отрезок, C — середина AB,

m — серединный перпендикуляр к AB,

AK=BK.

Доказать: K∈ m.

Доказательство:

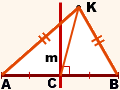Так как AK=BK (по условию), то треугольник AKB — равнобедренный с основанием AB (по определению). Так как C — середина AB, то KC — медиана треугольника AKB.

По свойству равнобедренного треугольника медиана, проведенная к основанию, является также его высотой, то есть

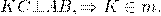
Вопрос 17.