Ортоцентр остроугольного треугольника

Задан треугольник , , , .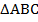

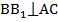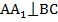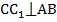Доказать, что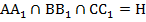

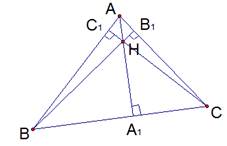
Рис. 2

Доказательство:

Проведем через вершины треугольника прямые, параллельные их противоположным сторонам:

через вершину А – прямую ,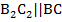

через вершину В – прямую ,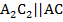

через вершину С – прямую .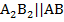

Получили новый треугольник , рассмотрим его свойства (см. Рис. 3).

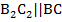, значит, 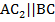. Аналогично 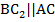. Отсюда четырехугольник 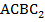является параллелограммом.

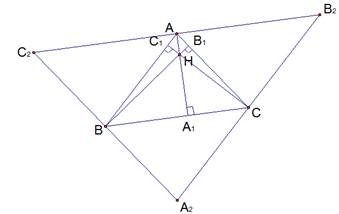
Рис. 3

Противоположные стороны параллелограмма попарно равны, отсюда , .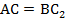

Аналогично 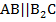, 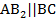по построению. Четырехугольник 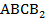– параллелограмм. Отсюда , .

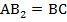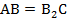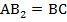, , отсюда 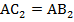. Таким образом, точка А – середина отрезка 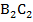, а значит, высота АА₁ в маленьком треугольнике – это серединный перпендикуляр в большом треугольнике.

Аналогичные действия можно выполнить для вершин В и С. Получим, что В – середина отрезка 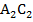, ВВ₁ – серединный перпендикуляр к стороне большого треугольника; С – середина 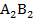, СС₁ – серединный перпендикуляр к стороне большого треугольника.

Мы знаем, что серединные перпендикуляры в большом треугольнике АА₁, ВВ₁, СС₁ пересекутся в одной точке – в точке Н. Также мы знаем, что эти серединные перпендикуляры являются высотами маленького треугольника, таким образом, высоты треугольника 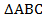пересекаются в одной точке Н, что и требовалось доказать.

В треугольнике все медианы и биссектрисы принадлежат треугольнику, чего нельзя сказать о высотах. В остроугольном треугольнике каждая высота принадлежит треугольнику.

Задача

Треугольник 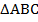остроугольный, АА₁ – высота (см. Рис. 4). Доказать, что основание высоты А₁ – это внутренняя точка отрезка ВС.

Дано: треугольник , , , ,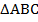

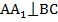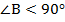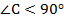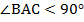
Доказать, что А₁ – это внутренняя точка отрезка ВС

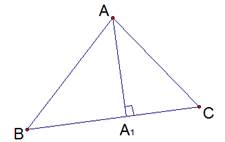
Рис. 4

Доказательство:

Докажем от противного: пусть АА₂ – это высота, и точка А₂ не является точкой отрезка ВС (см. Рис. 5).

Тогда угол 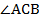– внешний угол для треугольника 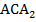. Внешний угол равен сумме внутренних углов треугольника, несмежных с ним, то есть углов 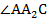и , то есть сумме прямого угла и какого-то острого угла, а данная сумма будет больше 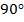, то есть угол 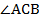будет тупой, что противоречит условию.

Рис. 5

Таким образом, основание высоты треугольника является внутренней точкой отрезка ВС.

Сделаем вывод: аналогичное доказательство можно выполнить для двух других высот остроугольного треугольника 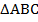, отсюда все три высоты остроугольного треугольника лежат внутри треугольника, точка их пересечения – ортоцентр – находится внутри треугольника.