
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неопределенный интеграл функции одной переменной
|
|
ТЕМАТИЧЕСКИЙ ПЛАН.
Тема 1. Неопределённый интеграл.
Тема 2. Определённый интеграл.
Тема 3. Дифференциальные уравнения.
СОДЕРЖАНИЕ КУРСА.
Тема 1. Первообразная функции и неопределённый интеграл. Основные свойства неопределённого интеграла. Интегралы основных элементарных функций. Интегрирование путём замены переменной. Метод интегрирования по частям. Интегрирование простейших рациональных дробей. Интегрирование тригонометрических функций.
Тема 2. Определённый интеграл и его свойства. Теорема о существовании определённого интеграла. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Методы замены переменной и интегрирование по частям в определённом интеграле. Геометрические приложения определённого интеграла. Несобственные интегралы. Приближённое вычисление определённых интегралов.
Тема 3. Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными. Линейные дифференциальные уравнения. Уравнения Бернулли. Линейные дифференциальные уравнения с постоянными коэффициентами.
ПЕРЕЧЕНЬ ЗАДАНИЙ.
Неопределенный интеграл функции одной переменной
Вычислить неопределенный интеграл методом непосредственного интегрирования (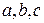 – произвольные константы, не равные нулю). Сделать проверку (посредством дифференцирования).
– произвольные константы, не равные нулю). Сделать проверку (посредством дифференцирования).
| № | Неопределенный интеграл |
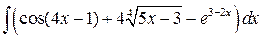 , , 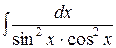 , , 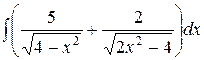 ; ;
| |
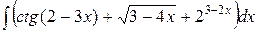 , , 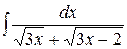 , , 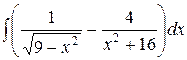 ; ;
| |
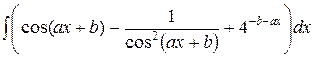 , , 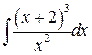 , , 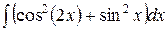 ; ;
| |
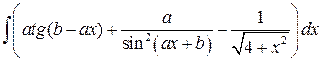 , , 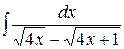 , , 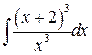 ; ;
| |
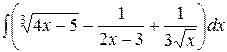 , , 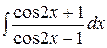 , , 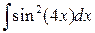 ; ;
| |
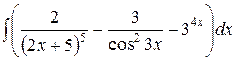 , , 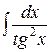 , , 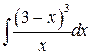 ; ;
| |
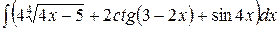 , , 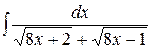 , , 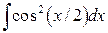 ; ;
| |
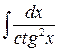 , , 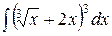 , , 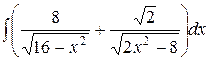 ; ;
| |
 , , 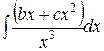 , , 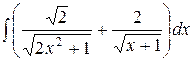 ; ;
| |
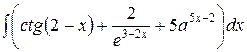 , , 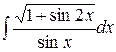 , , 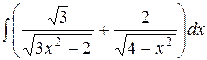 ; ;
| |
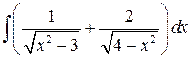 , , 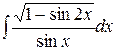 , , 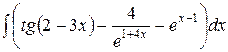 ; ;
| |
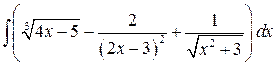 , , 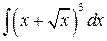 , , 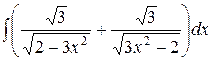 ; ;
| |
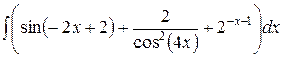 , , 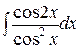 , , 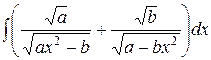 ; ;
| |
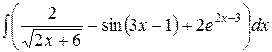 , , 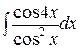 (указание: несколько раз воспользоваться формулой (указание: несколько раз воспользоваться формулой 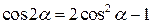 ), ), 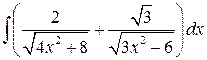 ; ;
| |
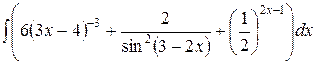 , , 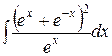 , , 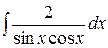 ; ;
| |
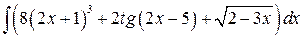 , , 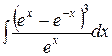 , , 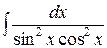 ; ;
| |
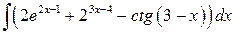 , , 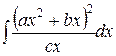 , , 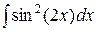 ; ;
| |
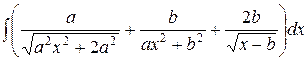 , , 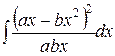 , , 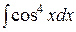 (указание: воспользоваться два раза формулой понижения степени (указание: воспользоваться два раза формулой понижения степени 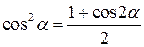 ); );
| |
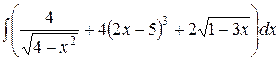 , , 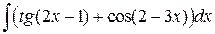 , , 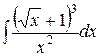 ; ;
| |
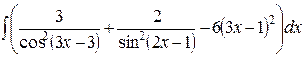 , , 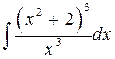 , , 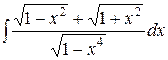 ; ;
| |
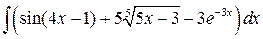 , , 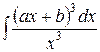 , , 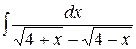 ; ;
| |
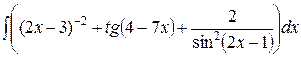 , , 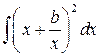 , , 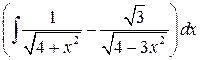 ; ;
| |
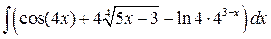 , , 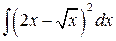 , , 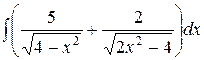 ; ;
| |
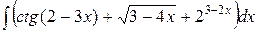 , , 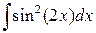 , , 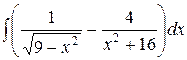 ; ;
| |
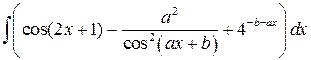 , , 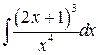 , , 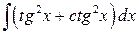 ; ;
| |
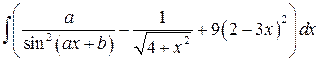 , , 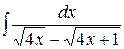 , , 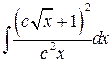 ; ;
| |
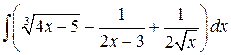 , , 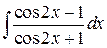 , , 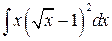 ; ;
| |
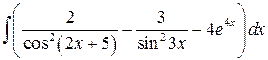 , , 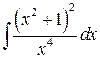 , , 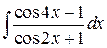 ; ;
| |
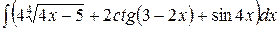 , , 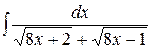 , , 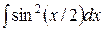 ; ;
| |
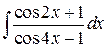 (указание: воспользоваться формулой (указание: воспользоваться формулой 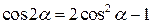 ), ),
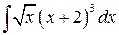 , , 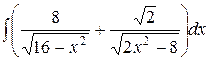 ; ;
| |
 , , 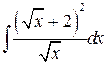 , , 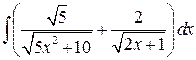 ; ;
| |
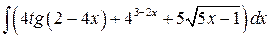 , , 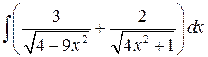 , , 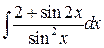 ; ;
| |
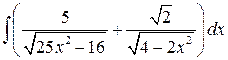 , , 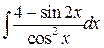 , , 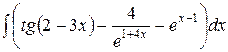 ; ;
| |
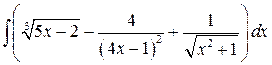 , , 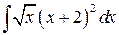 , ,
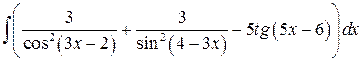 ; ;
| |
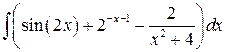 , , 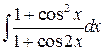 , , 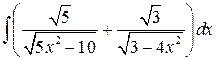 ; ;
| |
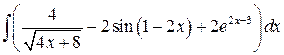 , , 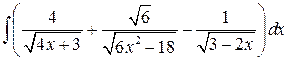 , ,
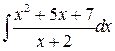 ; ;
| |
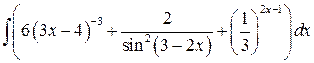 , , 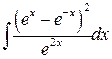 , ,
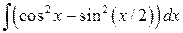 ; ;
| |
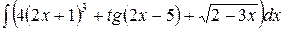 , , 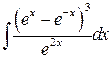 , , 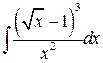 ; ;
| |
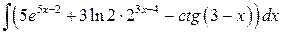 , , 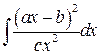 , , 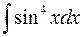 (указание: воспользоваться два раза формулой понижения степени (указание: воспользоваться два раза формулой понижения степени 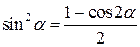 ); );
| |
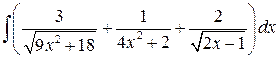 , , 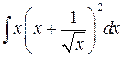 , , 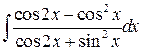 . .
|