Полный дифференциал. Производная по направлению и градиент.

Пусть область определения 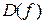функции 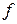содержит окрестность точки 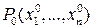, 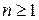. Функция 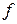называется дифференцируемой в точке 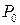, если для любых 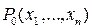из этой окрестности

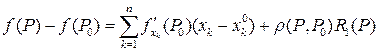(5.3),

где 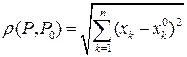и .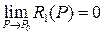

Линейная часть 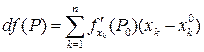приращения 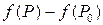называется полным дифференциалом функции 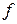в точке .

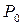График функции 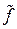, определяемой равенством (5.4), называется касательной плоскостью к графику функции 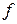в точке .

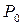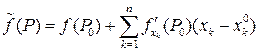(5.4)

Если 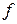дифференцируема в точке 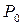, то 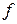непрерывна в 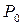и дифференцируема по каждому из переменных 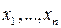. Однако если функция непрерывна и дифференцируема по каждому из переменных 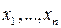в точке 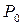, то она не обязательно дифференцируема в этой точке. Если же 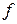непрерывно дифференцируема в точке 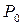, то 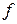дифференцируема в точке .

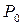Если 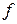дифференцируема в точке 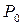, то существует производная по направлению функции 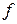в 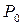относительно произвольного единичного вектора 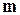, которая вычисляется по следующей формуле:

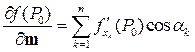(5.5),

где 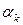- угол между вектором 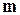и положительным направлением осей координат.

Если же 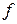дифференцируема по каждой из координат в точке 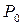, то вектор 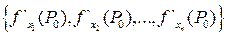называется градиентом функции 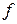в точке 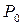и обозначается символом .

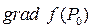Если 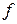дифференцируема в точке 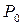, то в общем случае

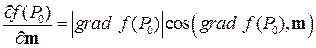(5.6),

где справа стоит скалярное произведение. Если при этом 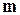- вектор в касательной плоскости к поверхности уровня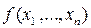 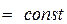, то

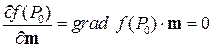(5.6*)

Свойства градиента:

1. Градиент функции 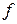перпендикулярен поверхности уровня .

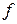2. Направление градиента есть направление наиболее быстрого роста функции (т.е. направление наибольшей производной по направлению).