Определенный интеграл функции одной переменной

Вычислить определенные интегралы.

№	Определенные интегралы
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; ;
	; ; ; ; .

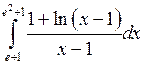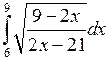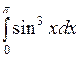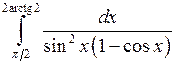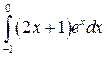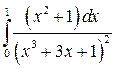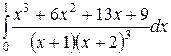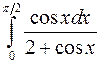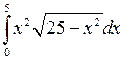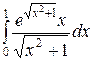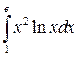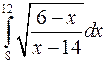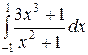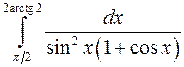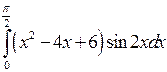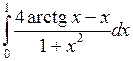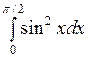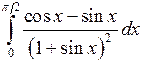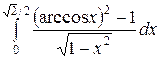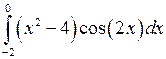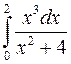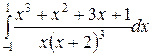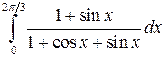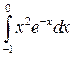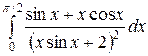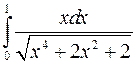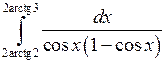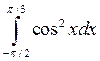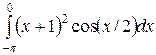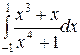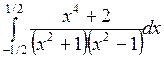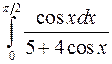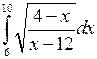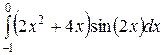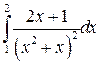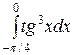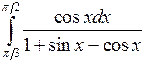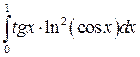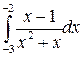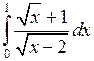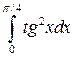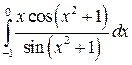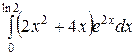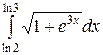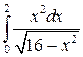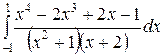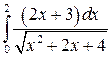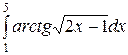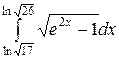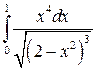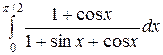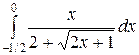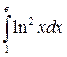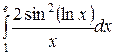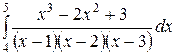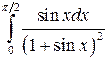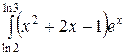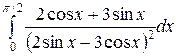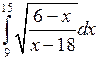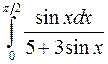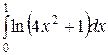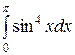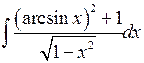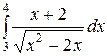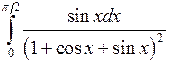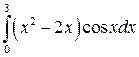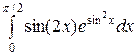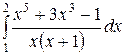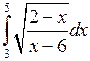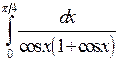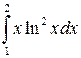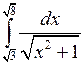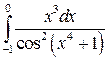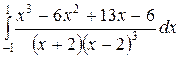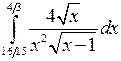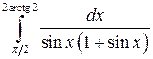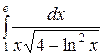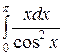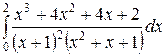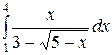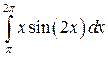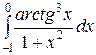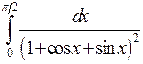
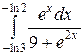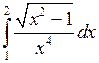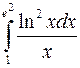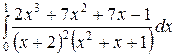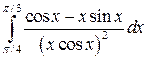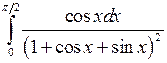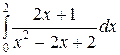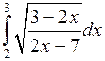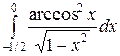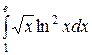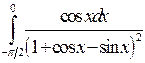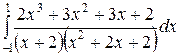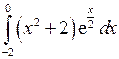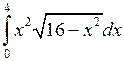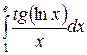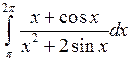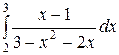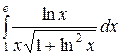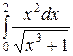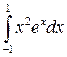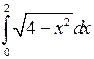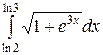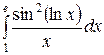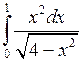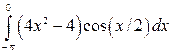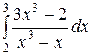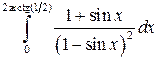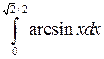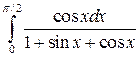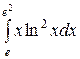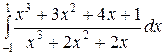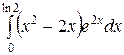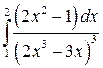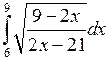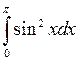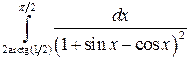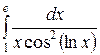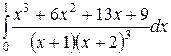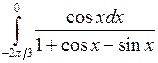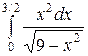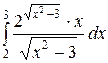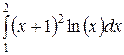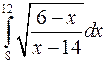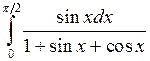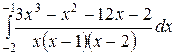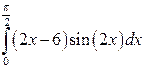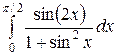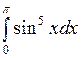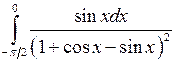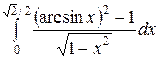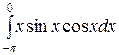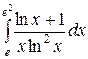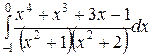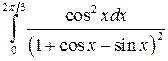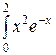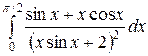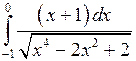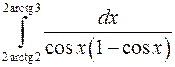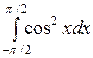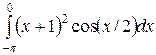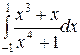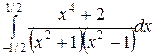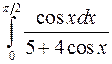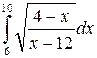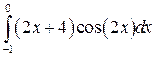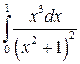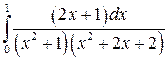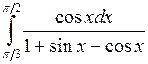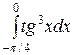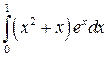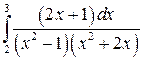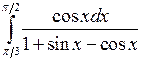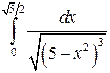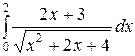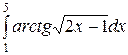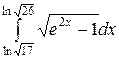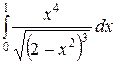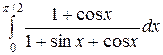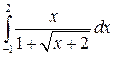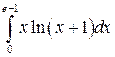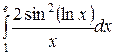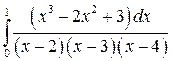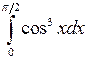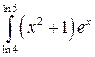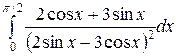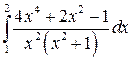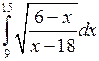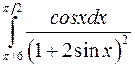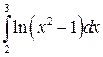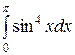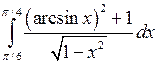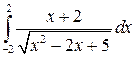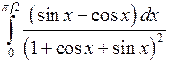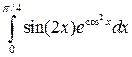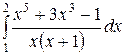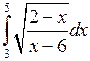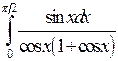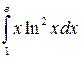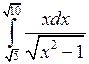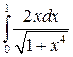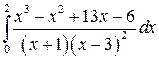Дифференциальное исчисление функции двух переменных

Задание 1. Для функции двух переменных 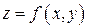, пользуясь правилами дифференцирования, найти производные: .

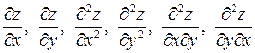№	Функция	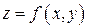№	Функция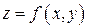
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
			;
	;		;
	;		.

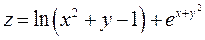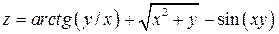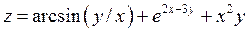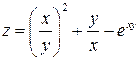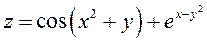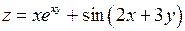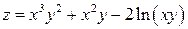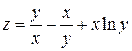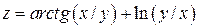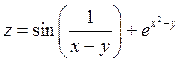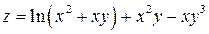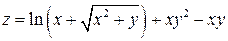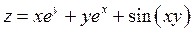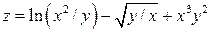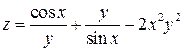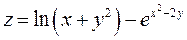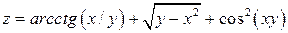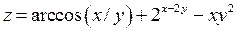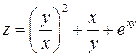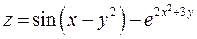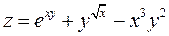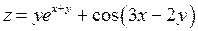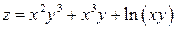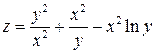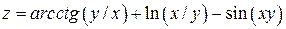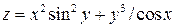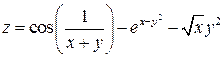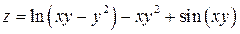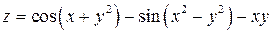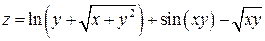
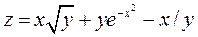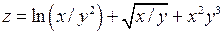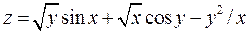Задание 2.Найти точки экстремума функции 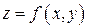. Характеризовать их тип.

№	Исследуемая функция	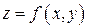№	Исследуемая функция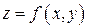
	;		;
	;		;
	;		;
	;		;
	;		;
	;		, ();
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	;		;
	, ;		;
	;		;
	, ;		;
	;		;
	;		;

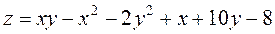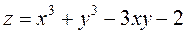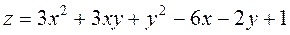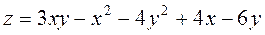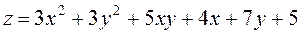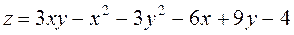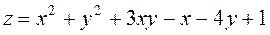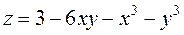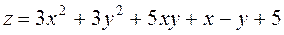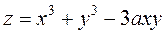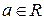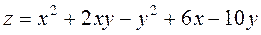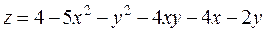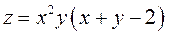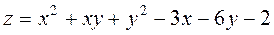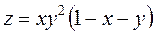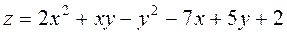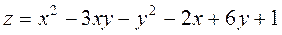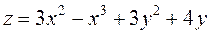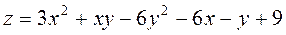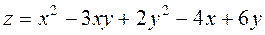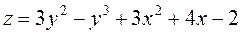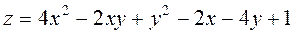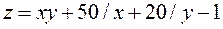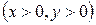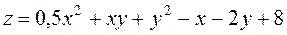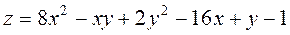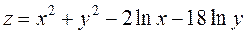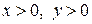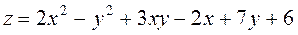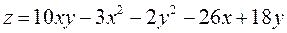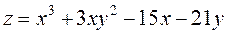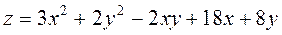МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ.

Неопределенный интеграл