Геометрические приложения определенного интеграла

1. Площадь криволинейной трапеции

Площадь фигуры, называемой криволинейной трапецией, лежащей под графиком 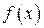и неотрицательной на отрезке 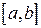равна

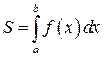
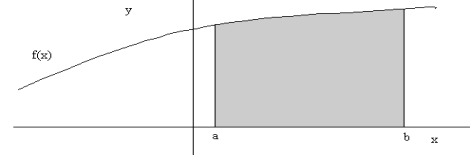
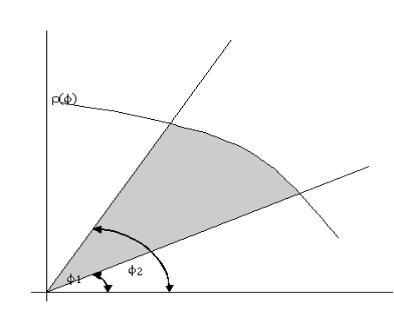
2. Площадь криволинейного сектора

Площадь фигуры, называемой криволинейным сектором, ограниченной графиком 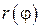и двумя лучами, составляющими с полярной осью углы 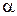и 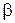имеет площадь

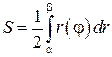
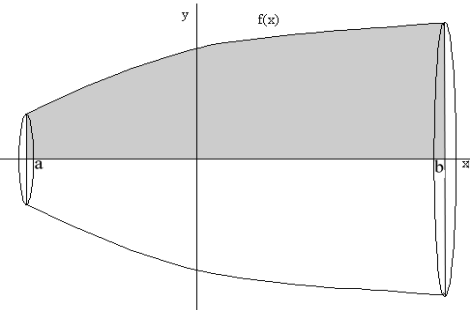
3. Вычисление объема вращения

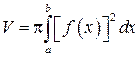
4. Длина дуги кривой.

Если плоская кривая L задана параметрически

, ,

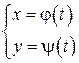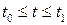причем 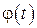и 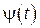- непрерывно дифференцируемые функции, то она имеет длину, вычисляемую по следующей формуле

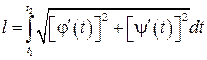
Если плоская кривая L – график непрерывно дифференцируемой функци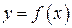и и 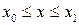, то длина этой кривой вычисляется по формуле

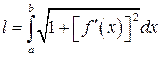
В полярных координатах

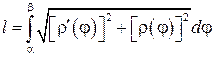
Примеры

Задача 1.Вычислить интеграл:

.

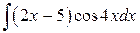Решение: применяя интегрирование по частям, получаем

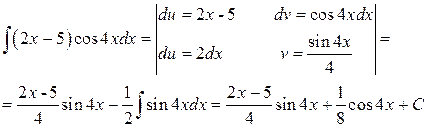
Задача №2:

Вычислить интеграл: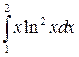

Решение:

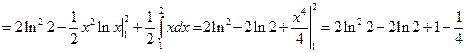
Задача №3:

Вычислить интеграл: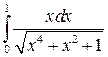

Решение:

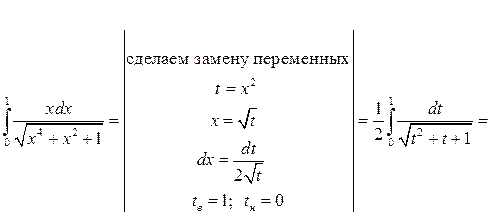
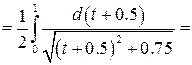
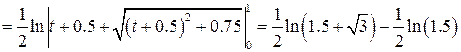
Задача №4:

Вычислить интеграл: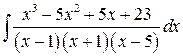

Решение:

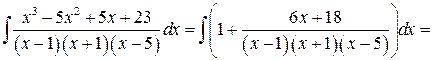
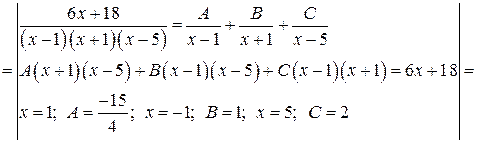
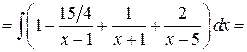
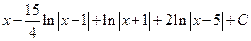
Задача №5:

Вычислить интеграл: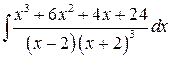

Решение:

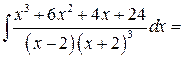
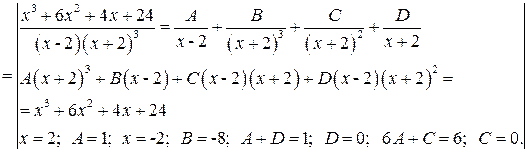
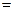
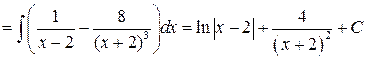
Задача №6:

Вычислить интеграл: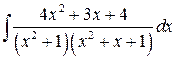

Решение:

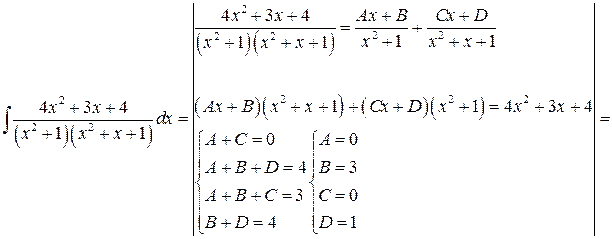
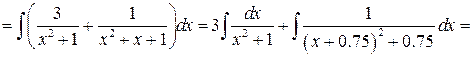
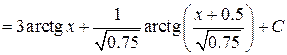
Задача №7:

Вычислить интеграл: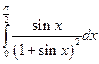

Решение:

Задача №8:

Вычислить интеграл: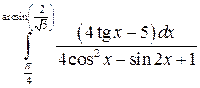

Решение:

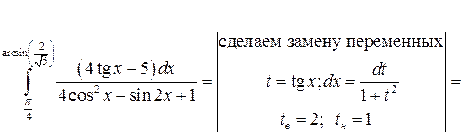
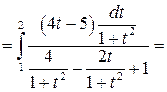
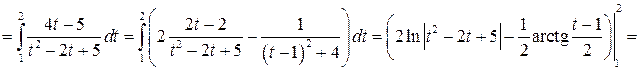
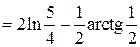
Задача №9:

Вычислить интеграл: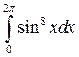

Решение:

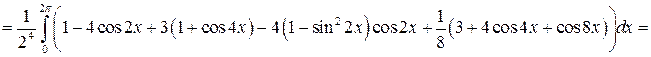
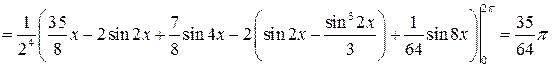
Задача №10:

Вычислить интеграл: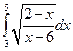

Решение:

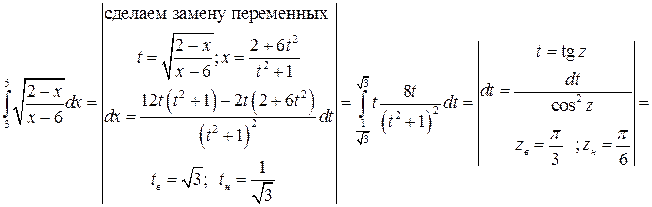
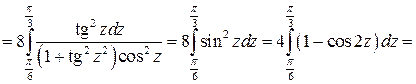
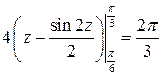
Задача №11:

Вычислить интеграл: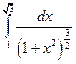

Решение:

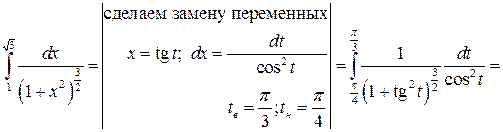
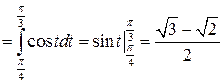
Задача №12:

Вычислить интеграл: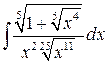

Решение:

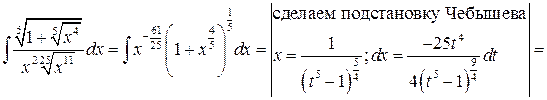
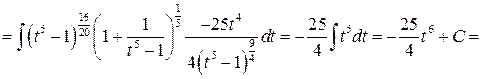
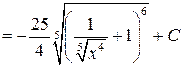
1. Функции многих переменных