
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бірінші және екінші тамаша шектер.
|
|
Бірінші тамаша шек. Қ ұ рамында тригонометриялық функциялар бар ө рнектердің шектерін есептегенде бірінші тамаша шекті қ олданады: 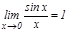 . Дә лелдеу: Радиусы бірге тең шең бер аламыз.
. Дә лелдеу: Радиусы бірге тең шең бер аламыз. 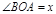 , сонда:
, сонда:
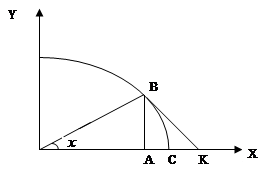
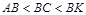 , мұ ндағ ы
, мұ ндағ ы
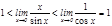
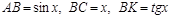
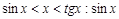
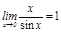
Шексіз аздарды салыстыру. Екі шексіз аз шамаларды салыстыру ү шін олардың қ атынасын қ арастырады. 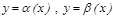 - ш.а.ш. болсын, яғ ни
- ш.а.ш. болсын, яғ ни 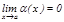 жә не
жә не 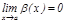 .
.
1. Егер 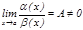 болса, онда
болса, онда 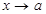 ұ мтылғ анда
ұ мтылғ анда 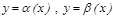 ш.а.ш.-ның аздық реттері бірдей дейді.
ш.а.ш.-ның аздық реттері бірдей дейді.
2. Егер 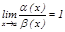 болса, онда
болса, онда 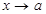 ұ мтылғ анда
ұ мтылғ анда 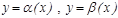 шексіз аз шамалар эквивалентті деп аталады жә не
шексіз аз шамалар эквивалентті деп аталады жә не 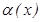 ~
~ 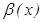 деп белгіленеді.
деп белгіленеді.
Мысал. 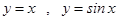 шексіз аздар
шексіз аздар 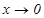 ұ мтылғ анда эквивалентті, бұ л бірінші тамаша шектің қ асиетінен шығ ады.
ұ мтылғ анда эквивалентті, бұ л бірінші тамаша шектің қ асиетінен шығ ады.
Теорема. 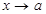 ұ мтылғ анда
ұ мтылғ анда 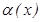 ш.а. болсын, онда:
ш.а. болсын, онда:
1. 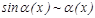 ; 2.
; 2. 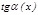 ~
~ 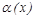 ;
;
3. 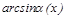 ~
~ 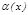 ; 4.
; 4. 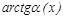 ~
~ 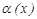 ;
;
5. 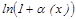 ~
~ 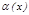 ; 6.
; 6. 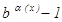 ~
~ 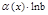 ,
, 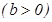 ;
;
Теорема. Егер ш.а.ф. –ды оларғ а эквивалентті функциялармен алмастырса, онда екі ш.а.ф. қ атынасының шегі ө згермейді.
Функцияның ү зіліссіздігі. Функцияның нү ктедегі ү зіліссіздігі ұ ғ ымын беру ү шін 3 шартты келтіреміз:
1. 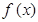 функциясы
функциясы 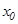 нү ктесінде анық талғ ан (яғ ни
нү ктесінде анық талғ ан (яғ ни 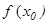 мә ні бар);
мә ні бар);
2. 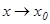 (
(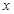 шамасы
шамасы 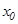 -ге ұ мтылғ анда) болғ анда
-ге ұ мтылғ анда) болғ анда 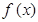 функциясының ақ ырлы шегі
функциясының ақ ырлы шегі 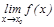 бар;
бар;
3. 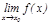 шегі функцияның
шегі функцияның 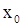 нү ктесіндегі мә ніне тең:
нү ктесіндегі мә ніне тең: 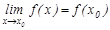
1− анық тама. Егер 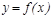 функциясы келтірілген ү ш шартты қ анағ аттандырса, онда оны
функциясы келтірілген ү ш шартты қ анағ аттандырса, онда оны 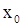 нү ктесінде ү зіліссіз дейді. Функцияның
нү ктесінде ү зіліссіз дейді. Функцияның 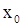 нү ктесіндегі ү зіліссіздігінің анық тамасының формуласын былай жазуғ а болады:
нү ктесіндегі ү зіліссіздігінің анық тамасының формуласын былай жазуғ а болады: 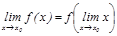 Функция
Функция 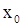 нү ктесінде ү зіліссіз болса, онда оның графигін
нү ктесінде ү зіліссіз болса, онда оның графигін 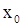 нү ктесі арқ ылы ү зіліссіз сызуғ а (қ арындашты қ ағ аздан алмай) болады. Енді ү зіліссіздіктің екінші анық тамасын берейік.
нү ктесі арқ ылы ү зіліссіз сызуғ а (қ арындашты қ ағ аздан алмай) болады. Енді ү зіліссіздіктің екінші анық тамасын берейік. 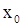 аргументіне
аргументіне 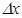 ө сімшесін берсек,
ө сімшесін берсек, 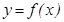 функциясы
функциясы 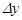 ө сімшесін алады. Ол
ө сімшесін алады. Ол 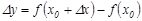 формуласымен анық талады.
формуласымен анық талады.
2− анық тама. Егер 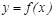 функциясы
функциясы 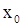 нү ктесінде анық талса жә не
нү ктесінде анық талса жә не 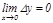 тең дігі орындалса, онда ол функцияны
тең дігі орындалса, онда ол функцияны 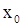 нү ктесінде ү зіліссіз дейді. Ү зіліссіздіктің осы екі анық тамасы ө зара эквивалентті. Егер
нү ктесінде ү зіліссіз дейді. Ү зіліссіздіктің осы екі анық тамасы ө зара эквивалентті. Егер 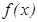 функциясы
функциясы 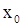 нү ктесінде ү зіліссіз болмаса, онда бұ л нү кте
нү ктесінде ү зіліссіз болмаса, онда бұ л нү кте 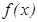 функциясының ү зіліс нү ктесі деп аталады. Ү зіліс нү ктесінің екі тү рі бар. Егер
функциясының ү зіліс нү ктесі деп аталады. Ү зіліс нү ктесінің екі тү рі бар. Егер 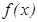 функциясың
функциясың 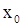 нү ктесінде оң жақ ты жә не сол жақ ты шектері бар болып, бірақ олар ө зара тең болмаса, онда
нү ктесінде оң жақ ты жә не сол жақ ты шектері бар болып, бірақ олар ө зара тең болмаса, онда 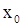 нү ктесі
нү ктесі 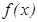 функциясының біріншітекті ү зіліс нү ктесі деп аталады. Егер оң жақ ты жә не сол жақ ты шектердің ең болмағ анда біреуі не шексіздікке тең болып, не жоқ болса, онда
функциясының біріншітекті ү зіліс нү ктесі деп аталады. Егер оң жақ ты жә не сол жақ ты шектердің ең болмағ анда біреуі не шексіздікке тең болып, не жоқ болса, онда 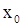 нү ктесі
нү ктесі 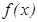 функциясының екіншітекті ү зіліс нү ктесі деп аталады. Егер
функциясының екіншітекті ү зіліс нү ктесі деп аталады. Егер 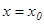 нү ктесінде ақ ырлы оң жақ ты жә не сол жақ ты шектер бар болып, бірақ олар осы нү ктедегі функцияның мә ніне тең болмаса, онда
нү ктесінде ақ ырлы оң жақ ты жә не сол жақ ты шектер бар болып, бірақ олар осы нү ктедегі функцияның мә ніне тең болмаса, онда 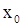 нү ктесі
нү ктесі 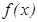 функциясының тү зетілетін ү зіліс нү ктесі деп аталады.
функциясының тү зетілетін ү зіліс нү ктесі деп аталады.
5-мысал. 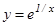 функциясы ү шін
функциясы ү шін 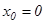 нү ктесі екінші текті ү зіліс нү ктесі болады, себебі
нү ктесі екінші текті ү зіліс нү ктесі болады, себебі
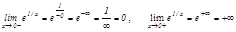

Егер 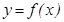 функциясы
функциясы 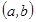 аралығ ының ә рбір нү ктесінде ү зіліссіз болса, онда оны
аралығ ының ә рбір нү ктесінде ү зіліссіз болса, онда оны 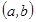 аралығ ында ү зіліссіз дейді. Егер
аралығ ында ү зіліссіз дейді. Егер 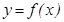 функциясы
функциясы 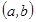 аралығ ында ү зіліссіз болып, ал
аралығ ында ү зіліссіз болып, ал 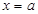 нү ктесінде оң жақ тан (яғ ни
нү ктесінде оң жақ тан (яғ ни 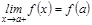 ), ал
), ал 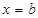 нү ктесінде сол жақ тан (яғ ни
нү ктесінде сол жақ тан (яғ ни 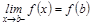 ) ү зіліссіз болса, онда
) ү зіліссіз болса, онда 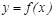 функциясын
функциясын 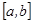 кесіндісінде ү зіліссіз дейді.
кесіндісінде ү зіліссіз дейді.