
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Туындының көмегімен функцияларды зерттеу және графигін салу
|
|
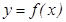 функциясы
функциясы 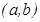 аралығ ында берілсін. Егер кез келген
аралығ ында берілсін. Егер кез келген 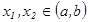 ү шін
ү шін 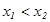 тең сіздігінен
тең сіздігінен 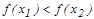 (
(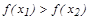 ) тең сіздігі шығ атын болса, онда
) тең сіздігі шығ атын болса, онда 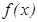 функциясы
функциясы 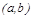 аралығ ында ө седі (кемиді) дейді.
аралығ ында ө седі (кемиді) дейді.
Теорема. Егер 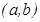 аралығ ында дифференциалданатын
аралығ ында дифференциалданатын 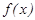 функциясының туындысы осы аралық та оң (теріс) болса, онда ол осы аралық та ө седі (кемиді). Демек, ө су немесе кему интервалында функцияның туындысы таң басын ө згертпейді.
функциясының туындысы осы аралық та оң (теріс) болса, онда ол осы аралық та ө седі (кемиді). Демек, ө су немесе кему интервалында функцияның туындысы таң басын ө згертпейді.
1-мысал. 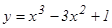 функцияның ө су жә не кему аралық тарын табу керек. Ол ү шін функция туындысының таң басының тұ рақ тылық интервалдарын анық таймыз
функцияның ө су жә не кему аралық тарын табу керек. Ол ү шін функция туындысының таң басының тұ рақ тылық интервалдарын анық таймыз 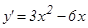 . Бұ л квадрат ү шмү шеліктің тү бірлері x1=0, x2=2. Сондық тан, егер
. Бұ л квадрат ү шмү шеліктің тү бірлері x1=0, x2=2. Сондық тан, егер 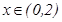 аралығ ында
аралығ ында 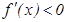 , демек
, демек 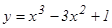 функциясы бұ л аралық та кемиді. Ал
функциясы бұ л аралық та кемиді. Ал 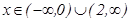 аралық тарында f'(x)> 0, демек бұ л аралық тарда функция ө седі.
аралық тарында f'(x)> 0, демек бұ л аралық тарда функция ө седі.
Теорема (экстремумның қ ажетті шарты). Егер дифференциалданатын 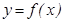 функциясының
функциясының 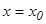 нү ктесінде экстремумы бар болса, онда сол нү ктеде
нү ктесінде экстремумы бар болса, онда сол нү ктеде 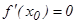 болады. Осы теоремадан мынадай қ орытындығ а келеміз: егер
болады. Осы теоремадан мынадай қ орытындығ а келеміз: егер 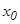 нү ктесінде функцияның экстремумы бар болса, онда ол нү ктеде оның туындысы нө лге тең, не ол нү ктеде туындысы болмауы мү мкін. Кері тұ жырым ә рқ ашан орындала бермейді. Мысалы,
нү ктесінде функцияның экстремумы бар болса, онда ол нү ктеде оның туындысы нө лге тең, не ол нү ктеде туындысы болмауы мү мкін. Кері тұ жырым ә рқ ашан орындала бермейді. Мысалы, 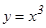 функциясының x0=0 нү ктесінде туындысы
функциясының x0=0 нү ктесінде туындысы 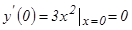 , ал бірақ ол нү ктеде функция не максимум, не минимум қ абылдамайды.
, ал бірақ ол нү ктеде функция не максимум, не минимум қ абылдамайды. 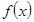 функциясының туындысы нө лге айналатын немесе тіпті болмайтын нү ктелерді кү дікті нү ктелер немесе «кризистік» нү ктелер деп атайды. Функцияның экстремумын осы кү дікті нү ктелердің арасынан іздеу керек.
функциясының туындысы нө лге айналатын немесе тіпті болмайтын нү ктелерді кү дікті нү ктелер немесе «кризистік» нү ктелер деп атайды. Функцияның экстремумын осы кү дікті нү ктелердің арасынан іздеу керек.
Теорема (экстремумнің жеткілікті шарты). Егер 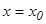 нү ктесінде
нү ктесінде 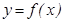 функциясының туындысы нө лге тең болса жә не
функциясының туындысы нө лге тең болса жә не 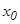 нү ктесінен ө ткенде
нү ктесінен ө ткенде 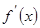 таң басын ө згертсе, онда
таң басын ө згертсе, онда 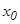 нү ктесі экстремум нү ктесі болады: 1) егер таң ба «плюс»-тен «минус»-ке ө згерсе, онда
нү ктесі экстремум нү ктесі болады: 1) егер таң ба «плюс»-тен «минус»-ке ө згерсе, онда 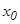 – максимум нү ктесі; 2) егер таң ба «минус»-тен «плюс»-ке ө згерсе, онда
– максимум нү ктесі; 2) егер таң ба «минус»-тен «плюс»-ке ө згерсе, онда 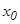 – минимум нү ктесі болады.
– минимум нү ктесі болады.
2-мысал. 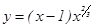 функцияны экстремумге зерттеп, ө су жә не кему аралық тарын анық тау керек. Функция туындысы
функцияны экстремумге зерттеп, ө су жә не кему аралық тарын анық тау керек. Функция туындысы 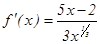 , осыдан
, осыдан 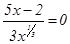 ,
, 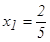 кү дікті нү ктесін табамыз.
кү дікті нү ктесін табамыз. 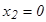 нү ктесінде функцияның туындысы болмайды, сондық тан ол да кү дікті нү кте. Интервалдар тә сілімен f '(x)- тің таң баларын анық таймыз. Функция
нү ктесінде функцияның туындысы болмайды, сондық тан ол да кү дікті нү кте. Интервалдар тә сілімен f '(x)- тің таң баларын анық таймыз. Функция 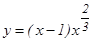 барлық нү ктелерде ү зіліссіз, жеткіліктілік шарт бойынша
барлық нү ктелерде ү зіліссіз, жеткіліктілік шарт бойынша 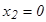 максимум нү ктесі, ал
максимум нү ктесі, ал 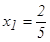 минимум нү ктесі. (–¥, 0) жә не
минимум нү ктесі. (–¥, 0) жә не 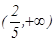 интервалдарда функция ө седі, ал
интервалдарда функция ө седі, ал 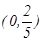 интервалда кемиді Зерттеу нә тижелерін таблицағ а жазамыз:
интервалда кемиді Зерттеу нә тижелерін таблицағ а жазамыз:
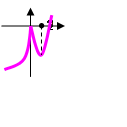 Функцияның екінші ретті туындысы қ олданылатын экстремумның тағ ы бір шартын келтірейік.
Функцияның екінші ретті туындысы қ олданылатын экстремумның тағ ы бір шартын келтірейік.
Теорема. 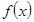 функциясының
функциясының 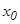 нү ктесінде бірінші жә не екінші туындылары бар болсын. Егер
нү ктесінде бірінші жә не екінші туындылары бар болсын. Егер 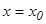 нү ктесінде
нү ктесінде 
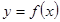 функциясының бірінші туындысы нө лге тең, яғ ни
функциясының бірінші туындысы нө лге тең, яғ ни 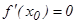 болса, ал екінші туындысы нө лден ерекше, яғ ни
болса, ал екінші туындысы нө лден ерекше, яғ ни 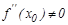 болса, онда
болса, онда 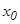 - экстремум нү ктесі болады:
- экстремум нү ктесі болады:
1) егер  болса, онда
болса, онда 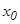 – минимум нү ктесі;
– минимум нү ктесі;
2) егер 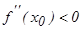 болса, онда
болса, онда 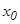 – максимум нү ктесі болады.
– максимум нү ктесі болады.
Функцияның кесіндідегі ең ү лкен жә не ең кіші мә ндері. Функция ө зінің ең ү лкен жә не ең кіші мә ндерін экстремум нү ктелерінде не кесіндісінің шеткі нү ктелерінде қ абылдауы мү мкін. Ең ү лкен жә не ең кіші мә ндерді табу ү шін алдымен функцияның кү дікті нү ктелерін (не туынды нө лге тең, не туынды жоқ нү ктелер) табу керек. Содан соң функцияның кү дікті нү ктелеріндегі жә не кесіндінің шеткі нү ктелеріндегі мә ндерін тауып, олардың ішінен ең ү лкен жә не ең кіші мә ндерді іздеу керек.
3-мысал. 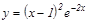 функциясының
функциясының 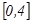 кесіндісіндегі ең ү лкен жіне ең кіші мә ндерін табу керек. Кү дікті нү ктелерді табамыз:
кесіндісіндегі ең ү лкен жіне ең кіші мә ндерін табу керек. Кү дікті нү ктелерді табамыз:
 Осыдан
Осыдан 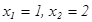 - кү дікті нү ктелер. Енді функцияның кү дікті нү ктелердегі жә не шеткі нү ктелердегі мә ндерін табамыз:
- кү дікті нү ктелер. Енді функцияның кү дікті нү ктелердегі жә не шеткі нү ктелердегі мә ндерін табамыз: 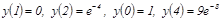 . Сонымен
. Сонымен 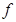 ү лкен
ү лкен 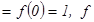 кіші
кіші 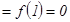 .
.