
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциалдық есептеулердің негізгі теоремалары
|
|
Анық тама. Егер 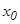 нү ктесінің бір маң айында
нү ктесінің бір маң айында 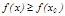
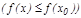 тең сіздігі орындалса, онда
тең сіздігі орындалса, онда 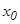 нү ктесін
нү ктесін 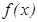 функциясының жергілікті минимум (максимум) нү ктесі деп атайды. Жергілікті минимум жә не жергілікті максимум нү ктелері жергілікті экстремум нү ктелері деп аталады. Ал осы нү ктелердегі функцияның мә ні функцияның экстремумы деп аталады.
функциясының жергілікті минимум (максимум) нү ктесі деп атайды. Жергілікті минимум жә не жергілікті максимум нү ктелері жергілікті экстремум нү ктелері деп аталады. Ал осы нү ктелердегі функцияның мә ні функцияның экстремумы деп аталады. 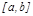 кесіндісінде анық талғ ан функцияның тек қ ана бір ең ү лкен жә не ең кіші мә ндері болады, ал максимумдар жә не минимумдер бірнеше болуы мү мкін. Функцияның кейбір максимумдары оның минимумдарынан кіші болуы да мү мкін.
кесіндісінде анық талғ ан функцияның тек қ ана бір ең ү лкен жә не ең кіші мә ндері болады, ал максимумдар жә не минимумдер бірнеше болуы мү мкін. Функцияның кейбір максимумдары оның минимумдарынан кіші болуы да мү мкін.
Ферма теоремасы. Егер  функциясы
функциясы 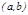 интервалында дифференциалданатын болса жә не
интервалында дифференциалданатын болса жә не 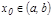 нү ктесінде ең ү лкен немесе ең кіші мә нін қ абылдайтын болса, онда функцияның туындысы бұ л нү ктеде нө лге тең, яғ ни
нү ктесінде ең ү лкен немесе ең кіші мә нін қ абылдайтын болса, онда функцияның туындысы бұ л нү ктеде нө лге тең, яғ ни 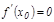 .
.
Геометриялық мағ ынасы: функцияның максимум жә не минимум нү ктелерінде жү ргізілген жанама 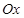 ө сіне параллель болады.
ө сіне параллель болады.
Ролль теоремасы. Егер 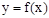 функциясы:
функциясы: 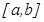 кесіндісінде ү зіліссіз болса,
кесіндісінде ү зіліссіз болса, 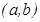 интервалында дифференциалданатын болса жә не
интервалында дифференциалданатын болса жә не 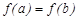 болса, онда ең болмағ анда бір
болса, онда ең болмағ анда бір  нү ктесі табылып,
нү ктесі табылып, 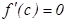 болады.
болады.
Геометриялық мағ ынасы: егер теорема шарттары толығ ымен орындалса, онда 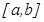 кесіндісінде жататын ең болмағ анда бір
кесіндісінде жататын ең болмағ анда бір 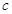 нү ктесі табылып, сол нү ктеде жү ргізілген жанама
нү ктесі табылып, сол нү ктеде жү ргізілген жанама 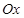 ө сіне параллель болады.
ө сіне параллель болады.
Kоши теоремасы. Егер 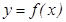 жә не
жә не 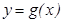 функциялары
функциялары 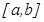 кесіндісінде ү зіліссіз болса,
кесіндісінде ү зіліссіз болса, 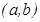 интервалында дифференциалданатын болса жә не
интервалында дифференциалданатын болса жә не 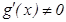
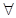
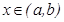 , онда ең болмағ анда бір
, онда ең болмағ анда бір  нү ктесі табылып
нү ктесі табылып 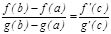 тең дігі орындалады.
тең дігі орындалады.
Л агранж теоремасы. Егер 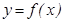 функциясы
функциясы  кесіндісінде ү зіліссіз болса,
кесіндісінде ү зіліссіз болса, 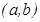 интервалында дифференциалданатын болса онда
интервалында дифференциалданатын болса онда 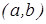 интервалында жататын
интервалында жататын 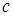 нү ктесі табылып,
нү ктесі табылып,  тең дігі орындалады.
тең дігі орындалады.
Геометриялық мағ ынасы: мына қ атынас 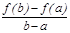
 кесіндісінде
кесіндісінде 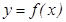 функциясының графигінің шеткі нү ктелерін қ осатын хорданың
функциясының графигінің шеткі нү ктелерін қ осатын хорданың 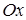 ө сінің оң бағ ытымен жасайтын бұ рыштың тангесіне тең, ал
ө сінің оң бағ ытымен жасайтын бұ рыштың тангесіне тең, ал 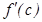
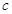 нү ктесіне жү ргізілген жанаманың
нү ктесіне жү ргізілген жанаманың 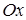 ө сінің оң бағ ытымен жасайтын бұ рышының тангенісіне тең. Лагранж теоремасы бойынша
ө сінің оң бағ ытымен жасайтын бұ рышының тангенісіне тең. Лагранж теоремасы бойынша  нү ктесінде олар ө зара тең болады, яғ ни қ июшы мен жанама параллель болады.
нү ктесінде олар ө зара тең болады, яғ ни қ июшы мен жанама параллель болады.
Лопиталь ережесі. Бұ л ереже 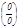 немесе
немесе 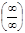 анық талмағ андық тарын есептеуге мү мкіндік береді.
анық талмағ андық тарын есептеуге мү мкіндік береді.
Теорема. Айталық, 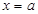 нү ктесінің маң айында
нү ктесінің маң айында 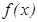 жә не
жә не 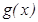 функциялары анық талғ ан жә не дифференциалданатын болсын (нү ктенің ө зінде бұ л шарттар орындалмауы да мү мкін) жә не
функциялары анық талғ ан жә не дифференциалданатын болсын (нү ктенің ө зінде бұ л шарттар орындалмауы да мү мкін) жә не  ,
, 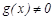 ,
, 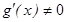 . Егер
. Егер 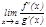 шегі бар болса, онда
шегі бар болса, онда 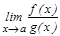 шегі бар болады жә не мына тең дік орындалады:
шегі бар болады жә не мына тең дік орындалады: 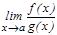 =
= 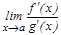 . Осы сияқ ты тұ жырымдар
. Осы сияқ ты тұ жырымдар 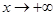 ,
,  ,
, 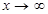 ,
,  ,
, 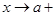 жағ дайларда да орынды.
жағ дайларда да орынды.
Функцияның дифференциалы. 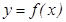 функциясының шектелген туындысы бар болсын, онда:
функциясының шектелген туындысы бар болсын, онда: 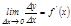 , демек
, демек 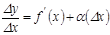
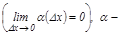 шексіз аз шама.
шексіз аз шама.
Онда функцияның ө сімшесі былай жазылады:  . Осы тең дікте екінші қ осылғ ыш
. Осы тең дікте екінші қ осылғ ыш 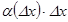 ,
, 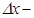 ке қ арағ анда жоғ арғ ы ретті шексіз аз шама болғ андық тан, бірінші қ осылғ ыш
ке қ арағ анда жоғ арғ ы ретті шексіз аз шама болғ андық тан, бірінші қ осылғ ыш 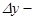 ке эквивалентті шама болады.
ке эквивалентті шама болады.
Анық тама. Функцияның туындысының аргументтің ө сімшесіне кө бейтіндісін дифференциал деп атайды жә не мына тү рде жазады: 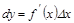 . Дербес жағ дайда, егер
. Дербес жағ дайда, егер 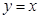 болса, онда
болса, онда 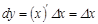 , осыдан
, осыдан 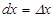 жә не осыны пайдаланып дифференциалдың формуласын былай жазуғ а болады:
жә не осыны пайдаланып дифференциалдың формуласын былай жазуғ а болады: 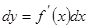 . Осыдан
. Осыдан 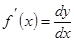 , яғ ни туынды функцияның дифференциалының аргумент дифференциалына бө лінген мә ніне тең.
, яғ ни туынды функцияның дифференциалының аргумент дифференциалына бө лінген мә ніне тең.
Дифференциалды есептеу ережесі. Айталық 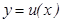 жә не
жә не 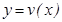 дифференциалданатын функциялар болсын,
дифференциалданатын функциялар болсын,
1) 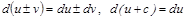 , мұ ндағ ы с – сан.
, мұ ндағ ы с – сан.
2) 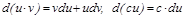 ,
,
3) 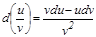 , егер
, егер 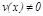 .
.
4) Егер 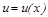 функциясы
функциясы 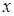 нү ктесінде дифференциалданатын, ал
нү ктесінде дифференциалданатын, ал 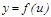
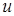 нү ктесінде дифференциалданатын болса, онда
нү ктесінде дифференциалданатын болса, онда 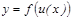 кү рделі функция ү шін,
кү рделі функция ү шін,  . Бұ л ережені бірінші дифференциал формасының инварианттығ ы деп атайды. Дифференциалды жуық тап есептеуге қ олдануғ а болады. Айталық,
. Бұ л ережені бірінші дифференциал формасының инварианттығ ы деп атайды. Дифференциалды жуық тап есептеуге қ олдануғ а болады. Айталық, 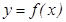 функциясы дифференциалданатын болсын, онда оның ө сімшесі:
функциясы дифференциалданатын болсын, онда оның ө сімшесі:
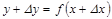 , осыдан
, осыдан 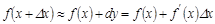 .
.
Егер 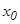 нү ктесінде функцияның мә ні берілсе, онда:
нү ктесінде функцияның мә ні берілсе, онда: 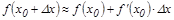 .
.