
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анықталмаған интегралдардың негізгі кестесі
|
|
1. 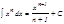 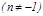 .
2. .
2. 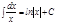 .
3. .
3. 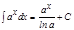 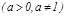 .
Дербес жағ дайда, .
Дербес жағ дайда, 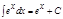 .
4. .
4. 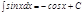 .
5. .
5. 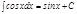 .
6. .
6. 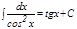 .
7. .
7. 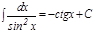 .
8. .
8. 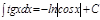 .
9. .
9. 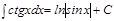 .
10. .
10. 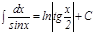 . .
|
11. 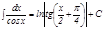 .
12. .
12. 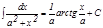 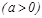 .
13. .
13. 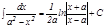 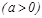 .
14. .
14. 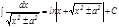 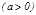 .
15. .
15. 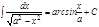 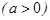 .
16. .
16. 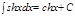 .
17. .
17. 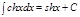 .
18. .
18. 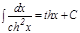 .
19. .
19. 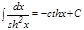 . .
|
Кестедегікезкелгенинтегралдытексеруү шінтең діктің оң жағ ынантуындыалукерек. Интегралдаудың негізгіә дістері
1. Анық талмағ ан интегралда айнымалыларды алмастыру. Айнымалыны алмастыру ә дісі мына формулағ а негізделген
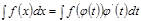
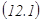
Мұ ндағ ы 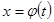 - берілген аралық та дифференциалданатын функция.Тиімді табылғ ан айнымалыны алмастыру формуласы берілген интегралды жең іл интегралдайтын интегралғ а, ал кейбір жағ дайларда таблицалық интегралғ а келтіреді.
- берілген аралық та дифференциалданатын функция.Тиімді табылғ ан айнымалыны алмастыру формуласы берілген интегралды жең іл интегралдайтын интегралғ а, ал кейбір жағ дайларда таблицалық интегралғ а келтіреді.
2. Дифференциал астына енгізу ә дісі. Бұ л ә діс айнымалыны ауыстыру сияқ ты жиі қ олданылады. Интеграл астындағ ы функцияның кө бейткіштерінің біреуін 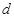 белгісінің астына жазамыз да, оны жаң а айнымалы ретінде қ арастырамыз. Еске сала кетейік,
белгісінің астына жазамыз да, оны жаң а айнымалы ретінде қ арастырамыз. Еске сала кетейік,  функциясын
функциясын 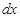 таң басының астына жазғ анда
таң басының астына жазғ анда 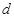 таң басынан кейін функцияның алғ ашқ ы функциясы жазылады, яғ ни
таң басынан кейін функцияның алғ ашқ ы функциясы жазылады, яғ ни 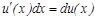 .
.
Салдар. Айталық 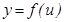 ү зіліссіз жә не
ү зіліссіз жә не 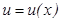 ү зіліссіз дифференциалданатын функциялар болсын, онда
ү зіліссіз дифференциалданатын функциялар болсын, онда
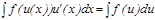
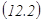
3. Бө ліктеп интегралдау ә дісі. Айталық, 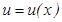 ,
, 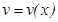 -дифференциалданатын функциялар болсын. Онда
-дифференциалданатын функциялар болсын. Онда 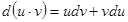 тең дігі орындалады. Немесе
тең дігі орындалады. Немесе 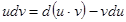 . Осы тең діктің екі жағ ынан интеграл алайық, сонда
. Осы тең діктің екі жағ ынан интеграл алайық, сонда 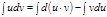 . Осыдан
. Осыдан
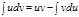

формуласын аламыз.  формуласын бө ліктеп интегралдау формуласы дейді. Кейбір жағ дайда бө ліктеп интегралдау формуласын қ олдану арқ ылы берілген интегралды алғ ашқ ығ а қ арағ анда анағ ұ рлым жең іл алынатын интегралғ а келтіруге болады.
формуласын бө ліктеп интегралдау формуласы дейді. Кейбір жағ дайда бө ліктеп интегралдау формуласын қ олдану арқ ылы берілген интегралды алғ ашқ ығ а қ арағ анда анағ ұ рлым жең іл алынатын интегралғ а келтіруге болады.
ында берілген 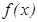 функциясы ү шін
функциясы ү шін
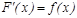 тең дігі орындалса, онда
тең дігі орындалса, онда