
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исық доғасының ұзындығы
|
|
а) Егер қ исық декарт координаттар жү йесінде 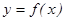 ,
, 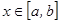 тең деуімен берілсе, онда қ исық тың доғ асының ұ зындығ ы мына формуламен есептелінеді:
тең деуімен берілсе, онда қ исық тың доғ асының ұ зындығ ы мына формуламен есептелінеді: 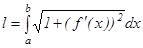 .
.
б) Егер қ исық параметрлік тү рде 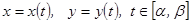 берілсе, онда қ исық тың доғ асының ұ зындығ ы мына формуламен есептелінеді:
берілсе, онда қ исық тың доғ асының ұ зындығ ы мына формуламен есептелінеді:  .
.
в) Егер қ исық сызық полярлық координаталар арқ ылы берілсе, яғ ни 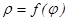 (
(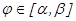 ), онда
), онда 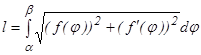 .
.
Айналу денесінің кө лемі. Ү зіліссіз 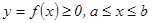 сызығ ымен жә не
сызығ ымен жә не 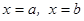 тү зулерімен шектелген қ исық сызық ты трапеция
тү зулерімен шектелген қ исық сызық ты трапеция 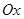 ө сінен айналуынан пайда болғ ан айналу денесінің кө лемі мына формуламен есептелінеді:
ө сінен айналуынан пайда болғ ан айналу денесінің кө лемі мына формуламен есептелінеді: 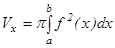 .
.
Айналу бетінің ауданын табу. Айталық, ү зіліссіз дифференциалданатын 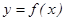 , (
, (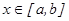 жә не
жә не 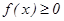 ) функциясының графигі
) функциясының графигі 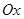 ө сінен айналсын. Пайда болғ ан айналу бетінің ауданы:
ө сінен айналсын. Пайда болғ ан айналу бетінің ауданы:
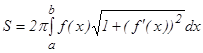
Меншіксіз интегралдар. Анық талғ ан интегралды қ арастырғ анда интегралдың тө менгі жә не жоғ ары шектері – ақ ырлы сандар жә не интеграл астындағ ы функция –интегралдау аралығ ында ақ ырлы функция болуын талап еттік. Егер осы қ ойылғ ан шарттардың біреуі орындалмаса, интеграл меншіксіз интеграл деп аталады.
1. Ақ ырсыз шектері бар меншіксіз интегралдар. Айталық, 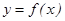 функциясы
функциясы 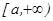 аралығ ында ү зіліссіз болсын. Осы функциядан
аралығ ында ү зіліссіз болсын. Осы функциядан 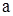 -дан
-дан 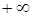 дейін алынғ ан меншіксіз интеграл деп мына шекті айтамыз:
дейін алынғ ан меншіксіз интеграл деп мына шекті айтамыз: 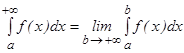 . Егер осы шек бар (санғ а тең) болса, онда меншіксіз интегралы жинақ ты, ал шегі жоқ немесе шексіздікке тең болса, онда интеграл жинақ сыз деп аталады. Егер
. Егер осы шек бар (санғ а тең) болса, онда меншіксіз интегралы жинақ ты, ал шегі жоқ немесе шексіздікке тең болса, онда интеграл жинақ сыз деп аталады. Егер 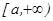 аралығ ында
аралығ ында 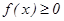 болса, онда мұ ндай интеграл шекаралары:
болса, онда мұ ндай интеграл шекаралары: 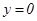 ,
, 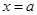
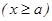 тү зулерімен жә не
тү зулерімен жә не 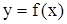 функциясының графигімен шектелген фигураның ауданын береді. Жинақ ты интеграл ү шін бұ л аудан шектеулі, ал жинақ сыз интеграл ү шін шектеусіз болады.
функциясының графигімен шектелген фигураның ауданын береді. Жинақ ты интеграл ү шін бұ л аудан шектеулі, ал жинақ сыз интеграл ү шін шектеусіз болады.
5-мысал. 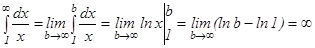 . Демек, интеграл жинақ сыз.
. Демек, интеграл жинақ сыз.
Айталық, 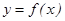 функциясы
функциясы 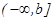 аралығ ында ү зіліссіз болсын. Сонда
аралығ ында ү зіліссіз болсын. Сонда 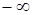 -тен
-тен 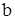 -ғ а дейінгі меншіксіз интеграл деп мына шекті айтамыз
-ғ а дейінгі меншіксіз интеграл деп мына шекті айтамыз 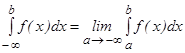 .
.
Мұ ндай интеграл (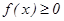 болғ анда) шекаралары
болғ анда) шекаралары 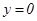 ,
, 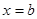
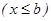 жә не
жә не 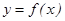 болғ ан фигураның ауданын ө рнектейді.
болғ ан фигураның ауданын ө рнектейді.
Егер 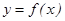 функциясы бү кіл сандар осінде ү зіліссіз болса, онда
функциясы бү кіл сандар осінде ү зіліссіз болса, онда 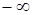 -тен
-тен 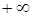 -ке дейінгі меншіксіз интеграл деп мына екі интегралдың қ осындысын айтамыз
-ке дейінгі меншіксіз интеграл деп мына екі интегралдың қ осындысын айтамыз
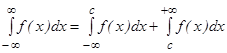
(мұ нда 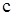 -кез келген сан). Бұ л анық тама
-кез келген сан). Бұ л анық тама 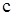 -ны таң дап алуғ а байланыссыз. Мұ ндағ ы екі интеграл да жинақ ты болса, онда ол интеграл жинақ ты деп аталады.
-ны таң дап алуғ а байланыссыз. Мұ ндағ ы екі интеграл да жинақ ты болса, онда ол интеграл жинақ ты деп аталады. 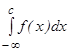 жә не
жә не 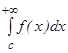 . Егер осы интегралдың біреуі жинақ сыз болса, онда
. Егер осы интегралдың біреуі жинақ сыз болса, онда 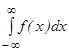 интегралы жинақ сыз деп аталады.
интегралы жинақ сыз деп аталады.