Жазық фигураның ауданын табу.

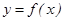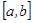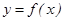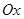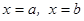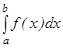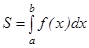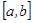а) функциясы кесіндісінде теріс емес жә не ү зіліссіз болсын. Онда жоғ арыдан функциясының графигімен, тө меннен ө сімен, ал бү йір жақ тарынан тү зулерімен қ оршалғ ан қ исық сызық ты трапецияның ауданы интегралына тең болады, яғ ни Егер кесіндісінде 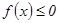болса, онда қ исық сызық ты трапеция 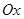ө сінің тө менгі жағ ына орналасқ ан жә не 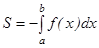болады.

1-мысал. 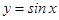синусоидасымен жә не 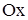осімен шектелген фигураның ауданын табу керек ().

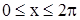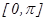аралығ ында 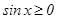, ал 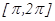аралығ ында 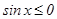болғ андық тан, берілген облыстың ауданын табайық

.

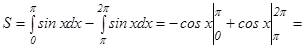
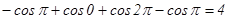б) 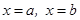тү зулерімен жә не 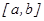аралығ ында ү зіліссіз 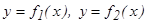(мұ ндағ ы 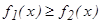) функциялардың графиктерімен шектелген фигураның ауданы мына формуламен табылады.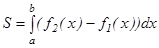

в) Егер 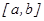кесіндісінде 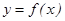функциясының графигі параметрлік функция тү рінде берілсін 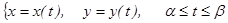мұ ндағ ы 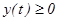ү зіліссіз, ал 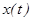функциясы 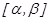кесіндісінде бір сарынды, ү зіліссіз дифференциалданатын функция, ал 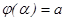, 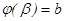болса, онда қ исық сызық ты трапецияның ауданы мына формуламен табылады .

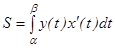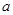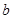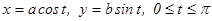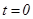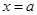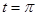2− мысал. Жарты ө стері жә не болатын эллипстің жоғ арғ ы жағ ындағ ы жарты бө лігінің параметрлік тең деуі былай беріледі: . Егер десек, онда , ал десек 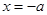тең болады. Сонда эллипстің ауданы былай табылады

.

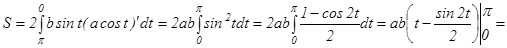
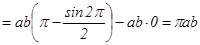Поляр координаттарындағ ы аудан. Координат тө бесінен шығ атын сә улелермен 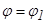жә не 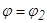(мұ ндағ ы 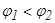) жә не теріс емес 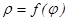функциясының 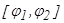кесіндідегі ү зіліссіз графигімен шектелген қ исық сызық ты ү шбұ рыштың ауданы мына формуламен есептелінеді:

3-мысал. 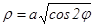қ исығ ымен шенелген облыстың ауданын табамыз. Бұ л қ исық Бернулли лемнискатасы деп аталады.

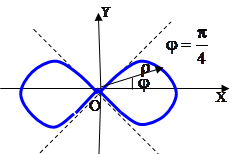
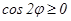шартынан интегралдау облысы табылады. Осыдан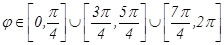 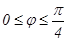ү шін бү кіл облыстың 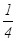-ін қ ұ райды.

.
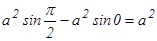