
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анықталған интегралдың анықтамасы. функциясы кесіндісінде анықталсын, мұнда . Төменгі амалдарды орындаймыз.
|
|
1. 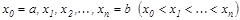 нү ктелерімен
нү ктелерімен 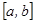 кесіндісін
кесіндісін  элементар кесінділерге (бө ліктерге) бө леміз:
элементар кесінділерге (бө ліктерге) бө леміз: 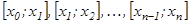
2. Ә рбір 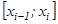 ,
, 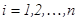 элементар кесіндінің ішінде жатқ ан, кез келген бір
элементар кесіндінің ішінде жатқ ан, кез келген бір 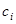

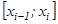 нү ктесін аламыз жә не осы нү ктедегі функцияның мә нін есептейміз, яғ ни
нү ктесін аламыз жә не осы нү ктедегі функцияның мә нін есептейміз, яғ ни 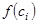 шамасын табамыз.
шамасын табамыз.
3. Функцияның табылғ ан 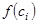 мә ндерін сә йкес элементар кесінділердің ұ зындығ ына, яғ ни
мә ндерін сә йкес элементар кесінділердің ұ зындығ ына, яғ ни 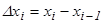 кө бейтеміз:
кө бейтеміз: 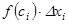 .
.
4. Барлық осындай кө бейтінділердің 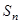 қ осындысын қ ұ рамыз:
қ осындысын қ ұ рамыз:
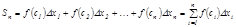
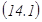
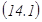 қ осындысы
қ осындысы 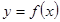 функциясының
функциясының 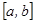 кесіндісіндегі интегралдық қ осындысы деп аталады. Элементар кесінділердің ең ү лкен ұ зындығ ын
кесіндісіндегі интегралдық қ осындысы деп аталады. Элементар кесінділердің ең ү лкен ұ зындығ ын  деп белгілейміз:
деп белгілейміз: 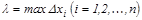 .
.
5. 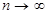 ұ мтылғ анда, яғ ни
ұ мтылғ анда, яғ ни 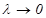 ұ мтылғ анда
ұ мтылғ анда 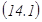 интегралдық қ осындысының шегін табамыз. Егер
интегралдық қ осындысының шегін табамыз. Егер 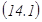 - интегралдық қ осындысы ү шін ақ ырлы шек бар болып, ол
- интегралдық қ осындысы ү шін ақ ырлы шек бар болып, ол 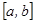 кесіндісін дербес бө ліктерге бө лу жолына жә не
кесіндісін дербес бө ліктерге бө лу жолына жә не 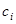 нү ктелерін таң дап алу тә сіліне тә уелсіз болса, онда ол шекті
нү ктелерін таң дап алу тә сіліне тә уелсіз болса, онда ол шекті 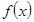 функциясының
функциясының 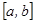 кесіндісіндегі анық талғ ан интегралы деп атайды жә не оны
кесіндісіндегі анық талғ ан интегралы деп атайды жә не оны 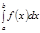 символымен белгілейді. Сонымен,
символымен белгілейді. Сонымен, 
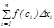
Мұ ндағ ы 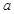 санын интегралдың тө менгі шегі, ал
санын интегралдың тө менгі шегі, ал 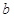 санын — жоғ ары шегі дейді.
санын — жоғ ары шегі дейді. 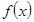 — интеграл астындағ ы функция,
— интеграл астындағ ы функция, 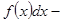 интеграл астындағ ы ө рнек деп аталады.
интеграл астындағ ы ө рнек деп аталады.
Егер 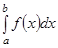 саны бар болса, онда
саны бар болса, онда 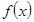 функциясы
функциясы 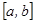 кесіндісінде интегралданатын функция деп аталады. Енді анық талғ ан интегралдың бар болуы туралы теореманы келтірейік.
кесіндісінде интегралданатын функция деп аталады. Енді анық талғ ан интегралдың бар болуы туралы теореманы келтірейік.
Теорема ( К оши). Егер 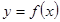 функциясы
функциясы 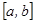 кесіндісінде ү зіліссіз болса, онда оның осы аралық та анық талғ ан интегралы
кесіндісінде ү зіліссіз болса, онда оның осы аралық та анық талғ ан интегралы 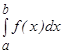 бар. Егер
бар. Егер 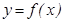 функциясының
функциясының 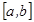 аралығ ында санаулы бірінші текті ү зіліс нү ктелері болса, онда бұ л функция
аралығ ында санаулы бірінші текті ү зіліс нү ктелері болса, онда бұ л функция 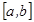 аралығ ында интегралданады.
аралығ ында интегралданады.
Анық талғ ан интегралдың анық тамасынан шығ атын оның кейбір қ асиеттері:
1. Анық талғ ан интеграл ө зінің интегралдау айнымаласына тә уелді емес, ол тек интегралдың шектері мен 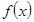 функциясынан тә уелді, яғ ни
функциясынан тә уелді, яғ ни 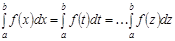 ,
,
2. Егер 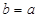 болса, онда
болса, онда 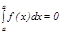
3. Кез келген нақ ты 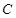 саны ү шін:
саны ү шін: 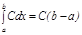
Анық талғ ан интегралдың қ асиеттері. Бұ л бө лімде интегралданатын функцияларды қ арастырамыз.
1. 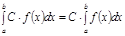 , мұ нда
, мұ нда 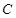 - нақ ты сан.
- нақ ты сан.
2. 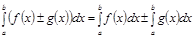 .
.
3. 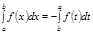
4. Егер  тең сіздігі орындалса, онда
тең сіздігі орындалса, онда 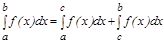 .
.
5. Егер 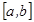 кесіндісінде
кесіндісінде 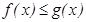 болса, онда
болса, онда 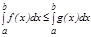 .
.
6. Орта мә н туралы теорема. Егер 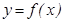 функциясы
функциясы 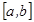 кесіндісінде ү зіліссіз болса, онда
кесіндісінде ү зіліссіз болса, онда 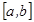 кесіндісінен
кесіндісінен 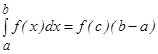 тең дігі орындалатындай
тең дігі орындалатындай 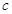 саны табылады.
саны табылады.
Ньютон – Лейбниц формуласы. Егер 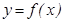 функциясы
функциясы 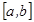 кесіндісінде интегралданатын болса, онда ол осы кесіндінің ішінде жатқ ан кез келген
кесіндісінде интегралданатын болса, онда ол осы кесіндінің ішінде жатқ ан кез келген 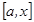 кесіндісінде де интегралданады.
кесіндісінде де интегралданады. 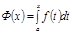 , мұ нда
, мұ нда 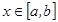 функциясын қ арастыралық.
функциясын қ арастыралық.
Теорема. Егер 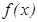 функциясы
функциясы 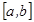 кесіндісінде ү зіліссіз болса, онда
кесіндісінде ү зіліссіз болса, онда 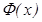 функциясы да
функциясы да 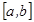 кесіндісінде ү зіліссіз болады.
кесіндісінде ү зіліссіз болады.
Теорема. 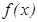 функциясы
функциясы 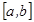 кесіндісінде ү зіліссіз болсын. Онда
кесіндісінде ү зіліссіз болсын. Онда
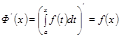
Салдар. 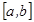 кесіндісінде ү зіліссіз болғ ан кез келген
кесіндісінде ү зіліссіз болғ ан кез келген 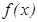 функциясының осы кесіндіде алғ ашқ ы функциясы бар, ол
функциясының осы кесіндіде алғ ашқ ы функциясы бар, ол 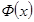 функциясына тең. Енді интегралды есептеудің негізгі формуласы Ньютон – Лейбниц формуласына кө шелік.
функциясына тең. Енді интегралды есептеудің негізгі формуласы Ньютон – Лейбниц формуласына кө шелік.
Негізгі теорема. 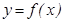 функциясы
функциясы 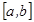 кесіндісінде ү зіліссіз жә не
кесіндісінде ү зіліссіз жә не 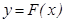
оның осы кесіндідегі алғ ашқ ы функциясы болсын. Онда
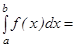
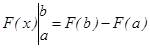
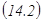
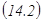 формуласы Ньютон- Л ейбниц формуласы деп аталады. Ньютон-Лейбниц формуласы анық талғ ан интегралды есептеу ү шін ө те қ олайлы қ ұ рал. Оны қ олдану ү шін интеграл астындағ ы жатқ ан функцияның бір алғ ашқ ы функциясын білу жеткілікті.
формуласы Ньютон- Л ейбниц формуласы деп аталады. Ньютон-Лейбниц формуласы анық талғ ан интегралды есептеу ү шін ө те қ олайлы қ ұ рал. Оны қ олдану ү шін интеграл астындағ ы жатқ ан функцияның бір алғ ашқ ы функциясын білу жеткілікті.