
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кейбір функцияларды интегралдау
|
|
Квадрат ү шмү шелігі бар функцияларды интегралдау. Мына тө мендегі интегралдарды табу ә дісін қ арастырайық 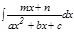 жә не
жә не 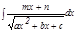 .
.
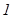 )
) 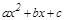 квадрат ү шмү шелігіндегі
квадрат ү шмү шелігіндегі 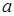 коэффициентін жақ ша алдына шығ арып, одан толық квадратты бө ліп аламыз;
коэффициентін жақ ша алдына шығ арып, одан толық квадратты бө ліп аламыз;
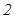 ) интегралғ а
) интегралғ а 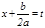 ,
, 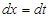 алмастыруын енгіземіз;
алмастыруын енгіземіз;
 ) Оны екі интегралдың қ осындысы етіп жазамыз. Сонда екі интегралымыз да кестелік интегралғ а келеді.
) Оны екі интегралдың қ осындысы етіп жазамыз. Сонда екі интегралымыз да кестелік интегралғ а келеді.
Рационал функцияларды интегралдау. Рационал бө лшекті интегралдау деп, 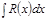 интегралын табуды айтады. Мұ ндағ ы
интегралын табуды айтады. Мұ ндағ ы 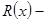 дұ рыс рационал бө лшек, яғ ни
дұ рыс рационал бө лшек, яғ ни 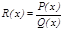
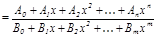 . Егер
. Егер  болса,
болса, 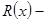 дұ рыс бө лшек деп, ал
дұ рыс бө лшек деп, ал 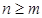 болса бұ рыс бө лшек деп аталады. Бұ рыс бө лшекті интегралдау ү шін алдымен алымын бө ліміне бө лу арқ ылы оны кө пмү шелік пен дұ рыс бө лшектің қ осындысына жіктейміз.
болса бұ рыс бө лшек деп аталады. Бұ рыс бө лшекті интегралдау ү шін алдымен алымын бө ліміне бө лу арқ ылы оны кө пмү шелік пен дұ рыс бө лшектің қ осындысына жіктейміз.
Теорема. Ә рбір дұ рыс рационал бө лшектімына қ арапайым бө лшектердің қ осындысы тү рінде жазуғ а болады:
1. 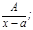 2.
2. 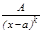
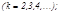 3.
3. 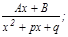 4.
4. 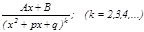 , мұ ндағ ы А, В - нақ тыкоэффициенттер;
, мұ ндағ ы А, В - нақ тыкоэффициенттер; 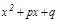 ү шмү шелігінің нақ ты тү бірлері жоқ (яғ ни
ү шмү шелігінің нақ ты тү бірлері жоқ (яғ ни 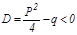 ). Қ арапайым бө лшектерді интегралдауды қ арастырайық.
). Қ арапайым бө лшектерді интегралдауды қ арастырайық.
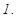
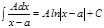 .
.
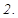
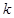
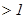 мә нінде
мә нінде 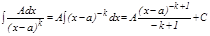 .
.
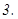
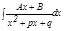 интегралдау ә дісі жоғ арыда қ арастырылғ ан.
интегралдау ә дісі жоғ арыда қ арастырылғ ан.
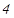 .
. 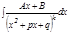 , мұ ндағ ы
, мұ ндағ ы 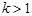 жә не бө ліміндегі квадрат ү шмү шеліктің дискриминанты
жә не бө ліміндегі квадрат ү шмү шеліктің дискриминанты 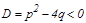 . Квадрат ү шмү шеліктен толық квадрат бө ліп алып
. Квадрат ү шмү шеліктен толық квадрат бө ліп алып 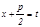 ,
, 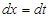 , алмастыруын жасаймыз. Сонда
, алмастыруын жасаймыз. Сонда 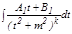 интегралын аламыз жә не оны екі интегралдардың қ осындысы тү рінде жазамыз. Бірінші интерал
интегралын аламыз жә не оны екі интегралдардың қ осындысы тү рінде жазамыз. Бірінші интерал 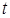 -ны дифференциал астына енгізу арқ ылы интегралданады:
-ны дифференциал астына енгізу арқ ылы интегралданады:
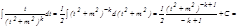
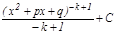 .
.
Ал екінші интегралды 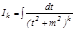 деп белгілеп, тө менгідей есептейміз:
деп белгілеп, тө менгідей есептейміз:
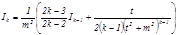
Бұ л формуланы реккуренттік формула деп атайды. Реккуренттік формула арқ ылы 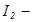 ні
ні 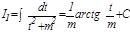 арқ ылы, ал
арқ ылы, ал 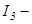 ті
ті 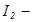 арқ ылы таба отырып, ең соң ында
арқ ылы таба отырып, ең соң ында 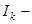 ны
ны 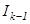 арқ ылы табамыз.
арқ ылы табамыз.
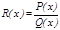 бө лшегінде
бө лшегінде  болсын. Ә рбір
болсын. Ә рбір 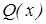 кө пмү шелігін бірінші жә не екінші дә режелі кө пмү шеліктердің кө бейтіндісіне жіктеп жазуғ а болады:
кө пмү шелігін бірінші жә не екінші дә режелі кө пмү шеліктердің кө бейтіндісіне жіктеп жазуғ а болады: 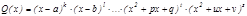 ,
,
мұ ндағ ы  бү тін сандар. Сонда дұ рыс бө лшек элементар бө лшектерге тө менгідей жіктелінеді:
бү тін сандар. Сонда дұ рыс бө лшек элементар бө лшектерге тө менгідей жіктелінеді:
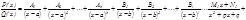
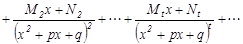
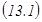
мұ ндағ ы 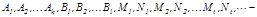 нақ ты сандар. Осы сандарды табу ү шін
нақ ты сандар. Осы сандарды табу ү шін 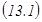 тең дігінің оң жағ ын ортақ бө лімге келтіреміз. Содан соң тең діктегі екі бө лшектің бө лімін алып тастасақ, екі жағ ында да кө пмү шелік шығ ады. Осы тең діктен бірдей дә режелі
тең дігінің оң жағ ын ортақ бө лімге келтіреміз. Содан соң тең діктегі екі бө лшектің бө лімін алып тастасақ, екі жағ ында да кө пмү шелік шығ ады. Осы тең діктен бірдей дә режелі 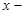 тің алдындағ ы коэффиценттерді тең естіре отырып, алгебралық тең деулер жү йесін қ ұ рамыз. Алынғ ан тең деулер жү йесінен
тің алдындағ ы коэффиценттерді тең естіре отырып, алгебралық тең деулер жү йесін қ ұ рамыз. Алынғ ан тең деулер жү йесінен 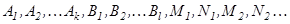 коэффиценттерінің мә ндерін тауып, оларды
коэффиценттерінің мә ндерін тауып, оларды 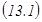 тең дігіне қ оямыз. Осылай рационал бө лшектің жіктеуін табамыз. Осы ә дісті анық талмағ ан коэффициенттер ә дісі дейді.
тең дігіне қ оямыз. Осылай рационал бө лшектің жіктеуін табамыз. Осы ә дісті анық талмағ ан коэффициенттер ә дісі дейді.
Кейбір иррационал функцияларды интегралдау. Иррационал функцияларды интегралдауда айнымалыны алмастыру арқ ылы рационал функцияның интегралына келуге болатын кейбір жағ дайларды қ арастырамыз. 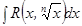 тү ріндегі интегралдар
тү ріндегі интегралдар 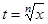 алмастыруы арқ ылы рационал функцияның интегралына келеді.
алмастыруы арқ ылы рационал функцияның интегралына келеді.
Қ арастырылғ ан интеграл 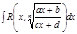 тү ріндегі интегралдың дербес тү рі
тү ріндегі интегралдың дербес тү рі
болады. Мұ нда 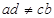 . Осы интегралды
. Осы интегралды 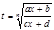 алмастыруы арқ ылы рационал функцияның интегралына келтіруге болады.
алмастыруы арқ ылы рационал функцияның интегралына келтіруге болады.
Тригонометриялық функцияларды интегралдау. Бұ л пунктте біз 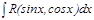 интегралын табуды қ арастырамыз. Берілген интеграл
интегралын табуды қ арастырамыз. Берілген интеграл 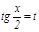 ә мбебап алмастыруы арқ ылы рационал функцияның интегралына келтіріледі. Шынында да
ә мбебап алмастыруы арқ ылы рационал функцияның интегралына келтіріледі. Шынында да
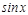
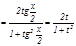 ,
, 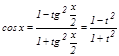 ,
, 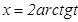 ,
, 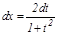
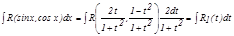 , мұ ндағ ы
, мұ ндағ ы 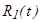 - рационал функция.
- рационал функция.
Бұ л ә дісті кө рсетілген кез келген интегралғ а қ олдануғ а болады, ал 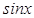 немесе
немесе 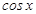 айнымалыларының дә режесі бірден жоғ ары болса қ олайсыз ү лкен ө рнектер шығ ады. Ондай жағ дайларда келесі ә дістерді қ олдану керек.
айнымалыларының дә режесі бірден жоғ ары болса қ олайсыз ү лкен ө рнектер шығ ады. Ондай жағ дайларда келесі ә дістерді қ олдану керек.
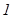 .
. 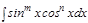 тү ріндегі интеграл.
тү ріндегі интеграл.
а) 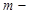 бү тін оң тақ сан болса, интеграл
бү тін оң тақ сан болса, интеграл 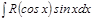 тү ріне келтіріліп,
тү ріне келтіріліп, 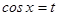 алмастырылуы жасалынады.
алмастырылуы жасалынады.
б) 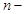 бү тін оң тақ сан болса, интеграл
бү тін оң тақ сан болса, интеграл 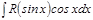 тү ріне келтіріліп,
тү ріне келтіріліп, 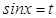 алмастырылуы жасалынады.
алмастырылуы жасалынады.
6- мысал. 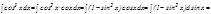
 .
.
в) 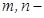 бү тін теріс емес жұ п сан болса,
бү тін теріс емес жұ п сан болса, 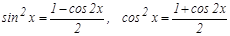 формулалары арқ ылы
формулалары арқ ылы 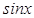 пен
пен 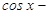 тің реттері тө мендетіледі.
тің реттері тө мендетіледі.
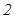 . Мына
. Мына 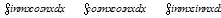 , мұ ндағ ы m, n – тұ рақ ты сандар, тү ріндегі интегралды алу ү шін тригонометрияның формулаларын:
, мұ ндағ ы m, n – тұ рақ ты сандар, тү ріндегі интегралды алу ү шін тригонометрияның формулаларын:
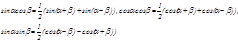
қ олдану жә не кө бейтінділерді қ осындығ а жіктеу арқ ылы берілген интегралды алу қ иынғ а тү спейді.