
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бір айнымалы функциялардың дифференциалдық есептеулері. Функцияның туындысы
|
|
Айталық, 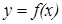 функциясы
функциясы  нү ктесінде жә не оның маң айында анық талғ ан болсын.
нү ктесінде жә не оның маң айында анық талғ ан болсын.
Анық тама. Аргумент 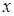 -тің
-тің 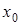 нү ктесіндегі ө сімшесі деп
нү ктесіндегі ө сімшесі деп 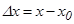 айырмасын атайды.
айырмасын атайды.
Анық тама. 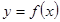 функцияның
функцияның  нү ктесіндегі ө сімшесі деп
нү ктесіндегі ө сімшесі деп 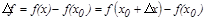 айырмасын айтады.
айырмасын айтады.
Анық тама. Егер 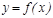 функциясы
функциясы  нү ктесінің маң айында анық талғ ан жә не
нү ктесінің маң айында анық талғ ан жә не 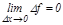 болса, онда ол
болса, онда ол  нү ктесінде ү зіліссіз деп аталады. Шындығ ында да
нү ктесінде ү зіліссіз деп аталады. Шындығ ында да 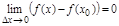
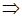
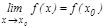 .
.
Анық тама. 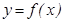 функциясының
функциясының 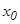 нү ктесіндегі туындысы деп
нү ктесіндегі туындысы деп
ақ ырлы шегін айтады.
Бұ л туынды мына символдардың бірімен белгіленеді: 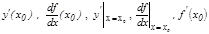 .
.
Егер 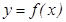 функциясының
функциясының 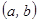 интервалының ә рбір нү ктесінде туындысы болса, онда оны осы интервалда дифференциалданады дейді. Туындыны табу амалын дифференциалдау дейді.
интервалының ә рбір нү ктесінде туындысы болса, онда оны осы интервалда дифференциалданады дейді. Туындыны табу амалын дифференциалдау дейді.
Теорема. Егер 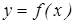 функциясы
функциясы  нү ктесінде дифференциалданатын функция болса, онда ол бұ л нү ктеде ү зіліссіз болады.
нү ктесінде дифференциалданатын функция болса, онда ол бұ л нү ктеде ү зіліссіз болады.
Ескерту: теорема керісінше дұ рыс емес.
Туындының геометриялық мағ анасы. Туындының геометриялық мағ ынасы: 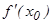 туындысы
туындысы 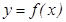 функциясының графигіне
функциясының графигіне 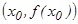 нү ктесінде жү ргізілген жанаманың бұ рыштық коэффициенті болады. Осы жанаманың тең деуін былай жазады:
нү ктесінде жү ргізілген жанаманың бұ рыштық коэффициенті болады. Осы жанаманың тең деуін былай жазады: 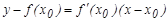 .Туындының механикалық мағ ынасы. Егер
.Туындының механикалық мағ ынасы. Егер 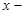 айнымалысын уақ ыт деп есептеп,
айнымалысын уақ ыт деп есептеп, 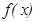 - функциясы дененің жү рген жолын сипаттаса, онда
- функциясы дененің жү рген жолын сипаттаса, онда 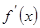 дененің
дененің 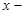 уақ ытындағ ы жылдамдығ ын білдіреді.
уақ ытындағ ы жылдамдығ ын білдіреді.
Дифференциалдаудың негізгі ережелері. Туындының анық тамасын пайдаланып, кейбір элементар (қ арапайым) функциялардың туындыларын есептейміз.
1. Кө рсеткішті функция 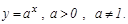
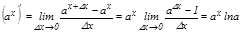 . Дербес жағ дайда
. Дербес жағ дайда 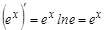 .
.
2. Тригонометриялық функциялар 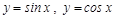 .
.
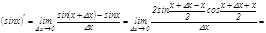
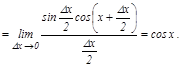 Дә л осылай
Дә л осылай 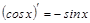 .
.
2. Дә режелік функция 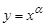 .
. 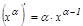
Дербес жағ дайда, 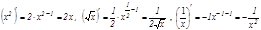 .
.
Теорема 1. (қ осындыны, кө бейтіндіні жә не қ атынасты дифференциалдау ережелері). Егер 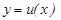 жә не
жә не 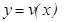 дифференцианалданатын болса, онда бұ л функциялардың қ осындысы, кө бейтіндісі жә не қ атынасы да (қ атынастың бө лімі
дифференцианалданатын болса, онда бұ л функциялардың қ осындысы, кө бейтіндісі жә не қ атынасы да (қ атынастың бө лімі 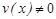 ) осы нү ктеде дифференцианалданады жә не мына формулалар орынды:
) осы нү ктеде дифференцианалданады жә не мына формулалар орынды:
1. 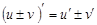 2.
2. 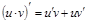 3.
3. 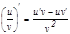 .
.
Кү рделі функцияның туындысы. 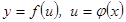 функциялары ү зіліссіз жә не дифференциалданатын функциялар болсын. Сонда кү рделі
функциялары ү зіліссіз жә не дифференциалданатын функциялар болсын. Сонда кү рделі 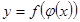 функциясының туындысы:
функциясының туындысы: 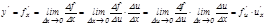 . Сонымен
. Сонымен 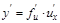 .
.
Кері функцияның туындысы. 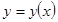 жә не оғ ан кері
жә не оғ ан кері 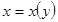 функциялары
функциялары 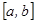 кесіндісінде ү зіліссіз жә не дифференциалданатын болсын. Сонда кері функцияның туындысы:
кесіндісінде ү зіліссіз жә не дифференциалданатын болсын. Сонда кері функцияның туындысы: 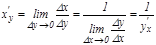 . Сонымен
. Сонымен 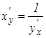 болады.
болады.
Негізгі элементар функциялар туындыларының кестесі
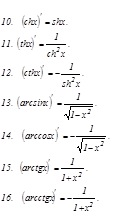
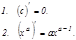
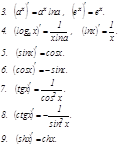 Жоғ арғ ы ретті туындылар мен дифференциалдар. Жоғ арғ ы ретті туындылар жә не дифференциалдар.
Жоғ арғ ы ретті туындылар мен дифференциалдар. Жоғ арғ ы ретті туындылар жә не дифференциалдар.
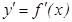 берілген
берілген 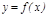 функциясының бірінші немесе бірінші ретті туындысы, ал функцияның ө зі нө лінші ретті туынды деп аталады.
функциясының бірінші немесе бірінші ретті туындысы, ал функцияның ө зі нө лінші ретті туынды деп аталады.
Анық тама. Функцияның 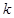 –ші ретті туындысы деп оның (
–ші ретті туындысы деп оның (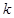 -1)-ші туындысының туындысын айтады
-1)-ші туындысының туындысын айтады 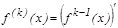 ,
, 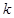 =1, 2, 3, …, егер олар бар болса, онда
=1, 2, 3, …, егер олар бар болса, онда 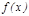 функциясы
функциясы 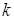 -рет дифференциалданатын функция деп аталады.
-рет дифференциалданатын функция деп аталады.
Мысал. 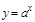 функциясы берілген. Бірінші туындысы
функциясы берілген. Бірінші туындысы 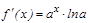 , екінші туындысы
, екінші туындысы 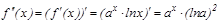 , ү шінші туындысы
, ү шінші туындысы 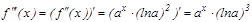 . Демек,
. Демек, 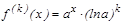 ,
, 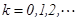 . Егер
. Егер 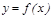 жә не
жә не 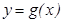 функциялары
функциялары 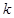 –рет дифференциалданатын болса, онда (
–рет дифференциалданатын болса, онда ( ), мына ережелер орынды:
), мына ережелер орынды: 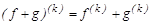 ,
, 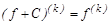 .
.
2. Лейбниц формуласы:
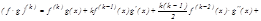
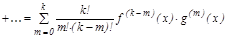 ;
; 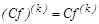 .
.
Айталық 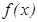 функциясы
функциясы 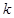 –рет дифференциалданатын болсын.
–рет дифференциалданатын болсын.
Анық тама. Функцияның 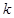 –ші дифференциалы деп оның (
–ші дифференциалы деп оның (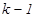 )–ші ретті дифференциалының дифференциалын айтады:
)–ші ретті дифференциалының дифференциалын айтады: 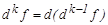 .
.
Дифференциалды есептеу формулаларын келтірейік:
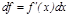 ,
,
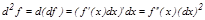 ,
,
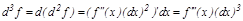
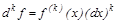 .
. 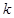 –шы ретті дифференциалдар ү шін мына ережелер орынды:
–шы ретті дифференциалдар ү шін мына ережелер орынды:
1) 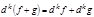 ,
, 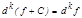 .
.
2) 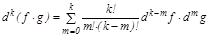 ,
, 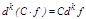 .
.
Ескерту: Жоғ арғ ы ретті 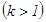 дифференциал формасы инвариантты емес.
дифференциал формасы инвариантты емес.