Постановка задачи. Рассмотрим двухсекторную экономическую модель, где

Рассмотрим двухсекторную экономическую модель, где

сектор 1 —производит инвестиционные товары, основные фонды, или капитал, фондообразующего сектора, осуществляющего инвестиции в собственное развитие и в развитие потребительского сектора (фазовая координата, заданная в начале свободная в конце, где она должна быть выбрана из соображений оптимальности);

сектор 2 — производит потребительские товары, основные фонды потребительского сектора, производящего товары

потребления (фазовая координата, отсчитываемая от достигнутого предпланового уровня);

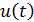— доля инвестиций, направляемых в потребительский сектор (управление);

Т — заданная протяженность интервала планирования, отсчитываемого от нуля.

Изменение производства в инвестиционном и потребительском секторах с течением времени может быть описано следующей системой дифференциальных уравнений

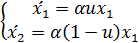
(1.1)

с начальными условиями

,

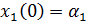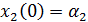
(1.2)

Где

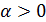– коэффициент степени воздействия на рост производства;

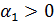– объем производства в начальный момент времени инвестиционных товаров;

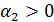– объем производства в начальный момент времени потребительских товаров;

– производство в 1-ом секторе;

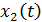– производство во 2-ом секторе.

Таким образом, увеличение производства в единицу времени в инвестиционном секторе, будет пропорционально увеличению производства в потребительском секторе.

На управление наложено ограничение 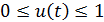, и если плановый период начинается пр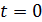и , и 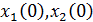изначально даны, то в этой ситуации задача оптимального управления может быть исследована.

В частном случае, рассмотрим задачу максимизации объема потребления в данный плановый период [0, Т], при 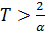, тогда получим систему (1.3):

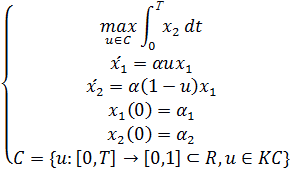
(1.3)