
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы Рунге-Кутты III,IV порядков
|
|
Дальнейшее улучшение точности решения ОДУ первого порядка возможно за счет увеличения точности приближенного вычисления интеграла в выражении.
Воспользовавшись формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши ОДУ первого порядка - широко используемого в вычислительной практике метода Рунге-Кутты.
В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подынтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [ xi+1, xi ]
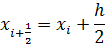
тогда можно переписать так:
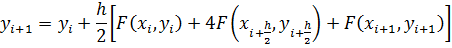
Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции yi+h/2и yi+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений
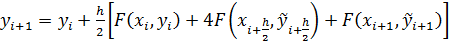
| (3.15) |
При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.
Алгоритм Рунге-Кутты третьего порядка - РК3 (погрешность порядка h3):
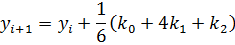
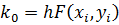
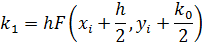
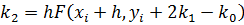
| (3.15) |
Алгоритм Рунге-Кутты четвертого порядка- РК4(погрешность порядка h4):
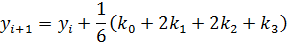
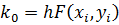
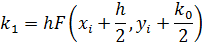
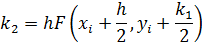
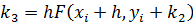
| (3.16) |
Алгоритмы третьего и четвертого порядков требуют на каждом шаге трех и четырех вычислений функции соответственно, но являются весьма точными.
Построим рекуррентные формулы по формуле по алгоритму РК3:
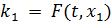
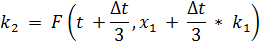
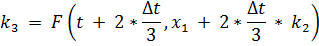
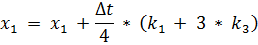
| (3.10) |
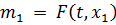
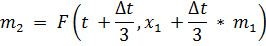
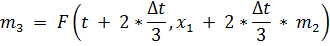
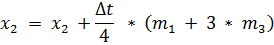
| (3.11) |
начальные условия:
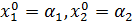
| (3.12) |
условия трансверсальности:
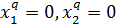
| (3.13) |
ограничение на управление:
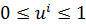
| (3.14) |
Гамильтониан Н:
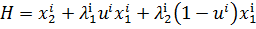 , при , при 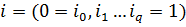
| (3.15) |
Условия стационарности по управлению и фазовым переменным строится аналогично методу Эйлера.
Для РК4 рекуррентные формулы строятся аналогично РК3, используя формулы (3.16).
3.3 Метод Адамса - Башфорта
Рассмотренные ранее методы (Эйлера, Рунге-Кутты) используют значение функции на одном предшествующем шаге, поэтому они относятся к так называемым одношаговым методам. Точность вычислений можно увеличить, если использовать при нахождении решения в некотором узле xi информацию о значениях функции, полученных в нескольких (k) предыдущих узлах сетки интегрирования (xi-1, xi-2… xi-k).
Если используются значения в k предыдущих узлах, то говорят о k-шаговом методе интегрирования уравнения. Одним из способов построения многошаговых методов заключается в следующем. По значениям функции, вычисленным в k предшествующих узлах, строится интерполяционный полином степени 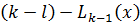 , который используется при интегрировании дифференциального уравнения по выражению. Интеграл при этом выражается через квадратурную формулу:
, который используется при интегрировании дифференциального уравнения по выражению. Интеграл при этом выражается через квадратурную формулу:
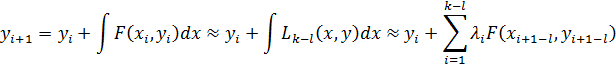
| (3.17) |
Значения квадратурных коэффициентов для k от 2 до 4 приведены в таблице.
| k | 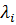
| |||
| 3/2 | -1/2 | |||
| 23/12 | -16/12 | 5/12 | ||
| 55/24 | -59/24 | 37/24 | -9/24 |
Полученное таким образом семейство формул называется явной k -шаговой схемой Адамса (методы Адамса-Башфорта).
Так как для вычислений по k -шаговой формуле необходимо знание значения функции в k узлах. Поэтому приходится (k-1) решение в первых узлах x1, x2, …, xk-1 получать с помощью какого-либо одношагового метода, например метода Рунге-Кутты 4–го порядка.