
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Эйлера. Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера
|
|
Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой y и независимой x переменных между узлами равномерной сетки:
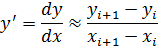
| (3.1) |
где yi+1 это искомое значение функции в точке xi+1 .
Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить yi+1 , если известно yi в точке хi:
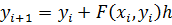
| (3.2) |
Сравнивая формулу Эйлера с общим выражением, полученным ранее, видно, что для приближенного вычисления интеграла в методе Эйлера используется простейшая формула интегрирования - формула прямоугольников по левому краю отрезка.
Построим рекуррентные формулы по формуле (3.2):
динамические ограничения:
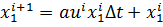
| (3.3) |
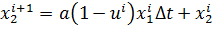
| (3.4) |
начальные условия:
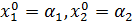
| (3.5) |
условия трансверсальности:
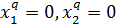
| (3.6) |
ограничение на управление:
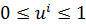
| (3.7) |
Гамильтониан Н:
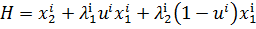 , при , при 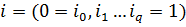
| (3.8) |
Функция Лагранжа:
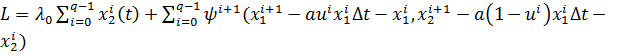
| (3.9) |
Условие стационарности по фазовым переменным:
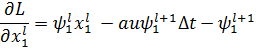
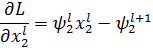
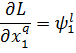
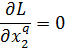
| (3.10) (3.11) (3.12) (3.13) |
Условие стационарности по управлению:
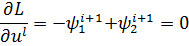
| (3.14) |