Численное решение

Будем рассматривать следующую задачу оптимального управления:

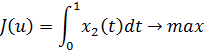
	(3.1)
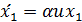
	(3.2)
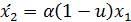
	(3.3)
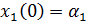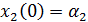
,	(3.4)
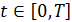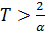
,	(3.5)
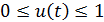
	(3.6)

Для численного интегрирования задачи Коши (3.1) при условии существования и единственности решения, известны методы: одношаговые Эйлера и Рунге-Кутта с модификациями, многошаговые типа Адамса и др.

Рассмотрим алгоритм решения задачи оптимального управления.

Алгоритм

Шаг 1: Подается начальный вектор управлений- u, начальные условия - 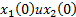, область поиска - 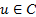, точность вычислений - , начальный и конечный момент времени - [t, T].

Шаг 2: Выбираем точку переключения

Шаг 3: При данном управлении решается задача Коши для системы дифференциальных уравнений, ищется траектория, вычисляется значение целевого функционала.

Шаг 4: Вызывается функция поиска приближенного решения.

Шаг 5: Проверка условий останова. Если условия не выполняются, переходим к шагу 2, иначе алгоритм прекращает свою работу.