Краевая задача принципа максимума

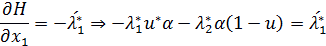
	(2.11)
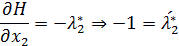
	(2.12)

Так как задача (2.1)-(2.5) со свободным правым концом, условия трансверсальности необходимы

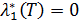
	(2.13)
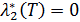
	(2.14)

Найдем максимальное положение управления 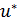в гамильтониане Н из (2.6) во всей области значений переменных x₁, x₂ , 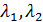. Рассмотрим зависимость Н по 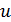, зависимость линейна, следовательно, максимум достигается на концах отрезка.

Проинтегрируем (2.12), и, используя условие трансверсальности (2.13) найдем константу, тогда 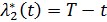. Кроме того (2.13) и (2.14) в уравнение (2.11) дают 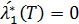. Заметим, что 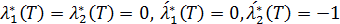. Из непрерывности множителей 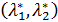следует, что существует 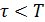такое, что

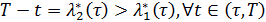
(2.15)

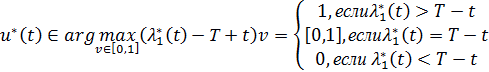
	(2.16)

Для устранения неоднозначности оптимального управления аналитического решения необходимо рассмотреть все случаи решения .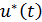

Найдем 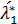и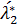

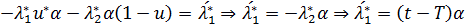
Проинтегрируем 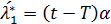по t и получим следующее:

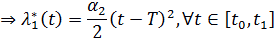
(2.17)

Вычисление показывает, что предположение (2.15) справедливо для 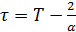. Поэтому давайте предположим, что существует точка 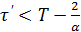такая, что

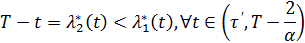
(2.18)

В силу (2.16) на интервале 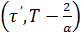мы получаем, что 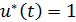. Теперь (2.11) дает, с учетом непрерывности 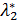в точке :

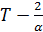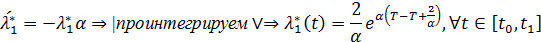
(2.19)

Легко проверить, что 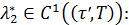поскольку 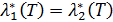и 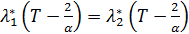, из выпуклости функци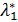и и 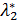следует, что предположение (2.18) выполняется с τ ’= 0.

В результате управление удалось построить как функцию времени:

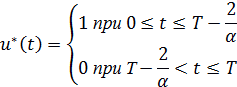
(2.20)

Полученную функцию 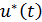подставим в дифференциальные уравнения (2.11), (2.12) и проинтегрируем их с заданными начальными условиями по участкам непрерывности функции 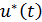, соблюдая непрерывность фазовых координат на границе соседних участков.

Сначала решим первое дифференциальное уравнение, поскольку оно не содержит 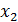, разделим переменные, проинтегрируем и выделим :

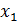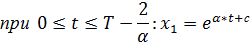
	(2.21)
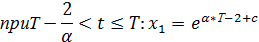
	(2.22)

Подставив исходное уравнение и используя начальные условия, получим, что

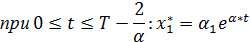
	(2.23)
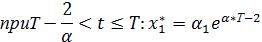
	(2.24)

Решая второе дифференциальное уравнение, проинтегрируем и выделим 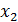, подставив вместо 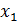полученное значение:

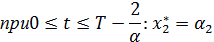
	(2.25)
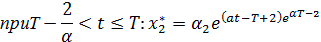
	(2.26)

Используя динамику и начальное условие на траектории, получим решения подозрительные на оптимальность:

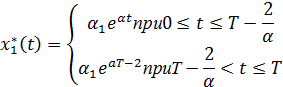
	(2.27)
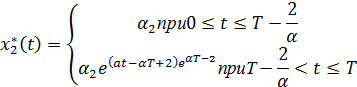
	(2.28)
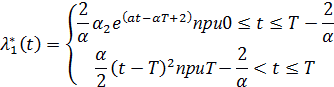
	(2.29)
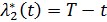
	(2.30)