
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Результаты решения задачи оптимального управления.
|
|
Для решения задачи оптимального управления на тему оптимальный режим управления двухсекторной модели в экономике разработано программное средство в среде Visual Studio 2013 на языке С# (приложение А). В качестве входных параметров будем рассматривать:
– коэффициент степени воздействия на рост производства;
– объем производства в начальный момент времени инвестиционных товаров;
– объем производства в начальный момент времени потребительских товаров;
– протяженность интервала планирования, отсчитываемого от нуля.
На рисунке (4.1) представлено решение задачи при следующих параметрах, методом Эйлера.
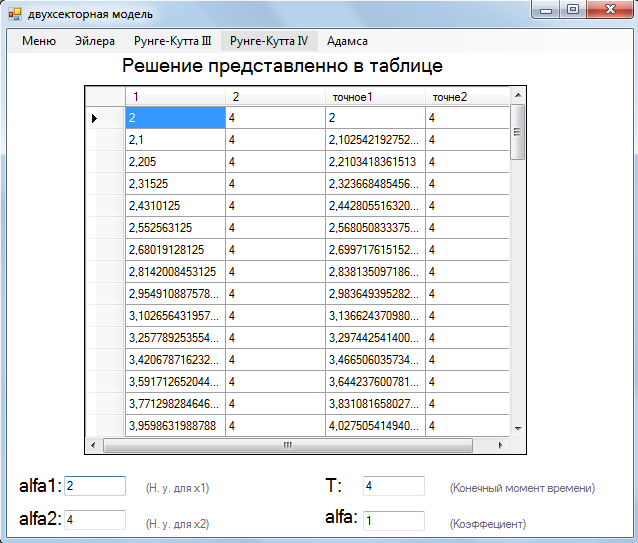
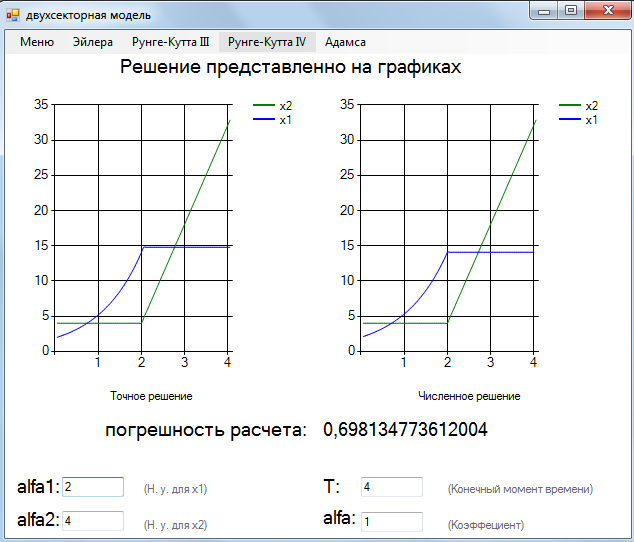
Рисунок 5.1 – Решение задачи оптимального управления методом Эйлера при 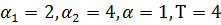 .
.
Для примера на рисунке (5.2) представлено решение задачи оптимального управления методом более высокого порядка – метод Рунге-Кутты IV порядка.
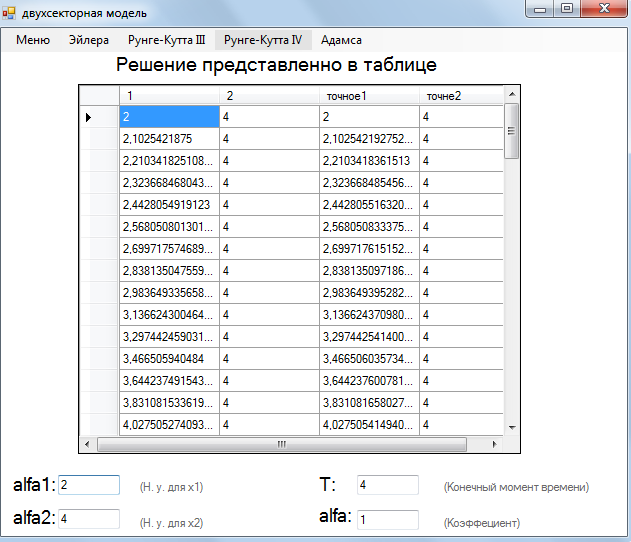
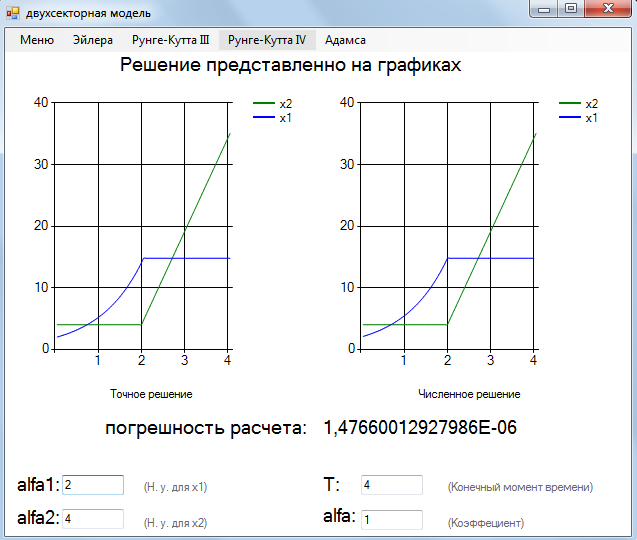
Рисунок 5.2 – Решение задачи оптимального управления методом Рунге-Кутты IV при 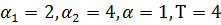 .
.
В начальный момент времени и до точки переключения (для наших параметров точка переключения 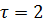 ) все основные фонды, или капитал фондообразующего сектора идут на собственное развитие и в развитие потребительского сектора. Выполнив предплановый уровень, то есть, начиная с момента точки переключения и до окончательного момента времени основные фонды, инвестиционные, производят товары потребления.
) все основные фонды, или капитал фондообразующего сектора идут на собственное развитие и в развитие потребительского сектора. Выполнив предплановый уровень, то есть, начиная с момента точки переключения и до окончательного момента времени основные фонды, инвестиционные, производят товары потребления.
На рисунке (5.3) представлено сопоставление методов. Из реализованных методов наибольшую точность имеет метод Адамса-Башфорта.
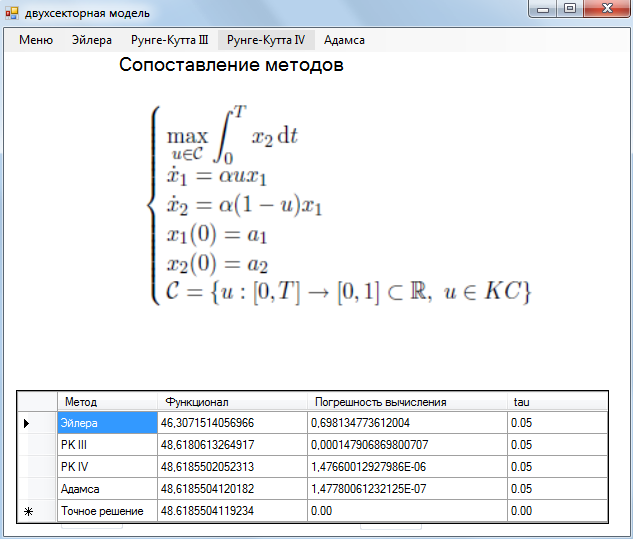
Рисунок 5.3 – Сопоставление полученных решений численными методами.
Заключение
Цель настоящей работы заключается в изучение математической модели двухсекторной экономики, а также реализация численных методов и алгоритмов для решения задачи оптимального режима управления двухсекторной модели в экономике.
Для достижения указанной цели были поставлены задачи. При решение задачи, применяя принцип максимума Понтрягина, были получены системы выражений для поиска оптимального решения.
Было доказано с помощью достаточного условия Эрроу, что полученная экстремаль это и есть оптимальное решение.
В рамках решения представления непрерывной задачи оптимального управления в дискретном виде были получены рекуррентные формулы для вычисления сопряженных переменных.
Разработано программное обеспечение для численного решения оптимального режима управления двухсекторной моделью экономики.