Числовая последовательность.

Если всякому натуральному числу (номеру места) по какому-нибудь закону однозначно поставлено в соответствие определенное число (член последовательности), говорят, что задана бесконечная числовая последовательность.

x₁, x₂, x₃, x₄, x₅, x₆, …., x_n – числовая последовательность.

x_n – n-ый член последовательности.

Последовательность – это частный случай функции. Ее областью определения является множество натуральных чисел. Последовательность можно задать формулой.

Пример:

1. x_n =2n – 1. Вычислим x₁ = 2•1 – 1=1, x₂ = 3, x₃ = 5 …. Т.е. последовательность 1, 3, 5, …

2. x_n = Последовательность 1/3, 2/5, 3/7, ….

Последовательность (n 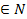) называется возрастающей, если для любого натурального n выполняется неравенство . Пример 1.

Последовательность (n 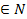) называется убывающей, если для любого натурального n выполняется неравенство . Пример 2.

Возрастающие и убывающие последовательности называются монотонными последовательностями.

Последовательность называется ограниченной, если существуют два числа m и M такие, что для всех n 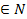выполняется неравенство, .

Пример: 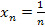- ограниченная , т.к. существуют 2 числа m=0 и M=1.

Предел числовой последовательности.

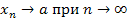Пусть номер n неограниченно увеличивается, т.е. стремится к бесконечности ( При этом соответствующие значения последовательности приближаются к некоторому числу a. Число a называется пределом последовательности и записывается или .

Число a называется пределом последовательности , если для любого сколь угодно малого положительного числа найдется такое натуральное число N, что при всех n > N выполняется неравенство , т.е. расстояние от N до a будут меньше .

Если последовательность имеет конечный предел, то она называется сходящейся.

Пример: предел последовательности 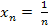стремится к 0, т.е. последовательность сходящаяся.

Если последовательность предела не имеет (либо предел равен ), то она называется расходящейся.

Пример: последовательность не имеет предела, т.е. она расходящаяся.