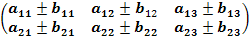Матрицы. Действия с матрицами.

Матрица – это прямоугольная таблица каких-либо элементов a _{i j ,}

где i – число строк, j – число столбцов.

У каждого числа свое местоположение, и переставлять их нельзя!

Матрицы обозначают прописными латинскими буквами A, B, C …

Когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Например, матрица размером 2× 2, 2× 3, 1× 4

А= - матрица состоит из 9 элементов, 3 строк и 3 столбцов

– единичная матрица – это матрица, сотоящая из 0 и 1.

нулевая матрица – это матрица, состоящая из 0.

Если в матрице один столбец или одна строка, то такие матрицы называют векторами: или

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной (3× 3, 2× 2).

Действия с матрицами.

1.Вынесение минуса из матрицы (внесение минуса в матрицу).

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:

2. Умножение матрицы на число.

чтобы умножить матрицу на число (целое или дробное, положительное или отрицательное), нужно каждый элемент матрицы умножить на данное число. Пример:

3.Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Пример: Транспонировать матрицу А=

А^t = – транспонированная матрица. Сумма (разность) матриц.

НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Для того чтобы сложить (вычесть) матрицы, необходимо сложить (вычесть) их соответствующие элементы:

А±B = ± =