Показатели корреляции при нелинейных соотношениях рассматриваемых признаков. Смысл средней ошибки аппроксимации.

Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:

Здесь общая дисперсия результативного признака y, - остаточная дисперсия, определяемая по уравнению нелинейной регрессии. Следует обратить внимание на то, что дисперсии вычисляются исходя из исходных значений результативного признака. Иначе говоря, при вычислении их следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Величина R находится в границах от 0 до 1, и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. Поскольку в расчете индекса корреляции используется соотношение остаточной и общей СКО, то R^2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R^2 для нелинейных связей называют индексом детерминации.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. у и ŷ _х. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у-ŷ _х) по каждому наблюдению представляет собой ошибку аппроксимации. Для того чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации. Она определяется как среднее отклонение полученных значений от фактических

Допустимая ошибка аппроисмации не должны превышать 10%.

20. Скорректированный коэффициент детерминации. В чем недостаток использования коэффициента детерминации при оценке общего качества линейной модели множественной регрессии?

Поскольку величина коэффициент детерминации R^2, как правило, увеличивается при добавлении объясняющей переменной к уравнению регрессии даже без достаточных на то оснований, скорректированный коэффициент компенсирует это увеличение путем наложения «штрафа» за увеличение числа независимых переменных. Скорректированный коэффициент детерминации:

.

По мере роста р увеличивается отношение р /(n-p -1) и, следовательно, возрастает размер корректировки коэффициента R² в сторону уменьшения.

Из формулы видно, что 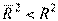при р > 1. С ростом р растет медленнее, чем R². Другими словами, он корректируется в сторону уменьшения с ростом числа объясняющих переменных. При этом только при R² =1.

Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых объясняющих переменных, что необязательно означает улучшение качества регрессионной модели. По этой причине, для устранения этого недостатка, на практике чаще используется скорректированный коэффициент детерминации.

Достоинство скорректированной R² относительно R²: его значение может уменьшаться при добавлении в модель новых факторов, не оказывающих существенного влияния на результат. Скорректированные коэффициенты в разных моделях с разным числом наблюдений ограниченно сравнимы.