
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование рациональных дробей с помощью разложения на простейшие дроби
|
|
Перед интегрированием рациональной дроби  следует выполнить следующие алгебраические преобразования и вычисления:
следует выполнить следующие алгебраические преобразования и вычисления:
1) если дана неправильная рациональная дробь, то следует выделить из нее целую часть (разделить числитель на знаменатель дроби), т.е. представить дробь в виде

 (1)
(1)
где М(х) – многочлен, а  - правильная рациональная дробь,
- правильная рациональная дробь, 
2) разложить знаменатель дроби на линейные и квадратичные множители:

где трехчлен  имеет комплексные сопряженные корни;
имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби

 (2)
(2)
4) вычислить неизвестные коэффициенты  применив метод неопределенных коэффициентов, который можно реализовать тремя способами.
применив метод неопределенных коэффициентов, который можно реализовать тремя способами.
1 способ. Надо привести (2) к общему знаменателю, приравнивать коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.
2 способ. Можно определить коэффициенты и другим способом, придавая в полученном тождестве переменной х произвольные числовые значения.
3 способ. Часто применяется комбинированный способ – оба способа вычисления коэффициентов комбинируются.
Таким образом, интегрирование рациональной дроби сводится к нахождению интегралов от многочлена и от простейших рациональных дробей.
Пример1. Вычислить интеграл 
Решение: Подынтегральная функция правильная рациональная дробь. Разложим на простейшие дроби 


Сравнивая коэффициенты при 
 и
и 


Решая эту систему найдем  поэтому искомое разложение
поэтому искомое разложение
имеет вид 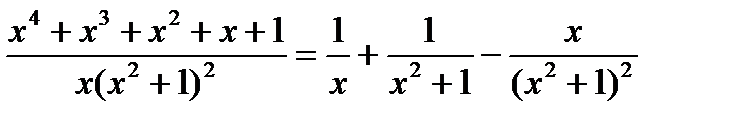
Следовательно
