Дифференциальные уравнения 2-го порядка

Определение 1. Дифференциальные уравнения 2-го порядка имеет вид: (1) или (2).

Определение 2. Решением уравнения (1) называется функция , дважды дифференцируемая, которая обращает (1) в тождество.

Определение 3. Общим решением дифференциального уравнения (1) называется функция , зависящая от произвольных постоянных 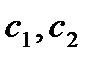которая

1) Удовлетворяет уравнению (1) при любых значениях

2) При заданных начальных условиях, постоянные можно подобрать так, что функция будет удовлетворять этим условиям.

Определение 4. Частным решением уравнения (1) называется всякое решение, полученное из общего решения при конкретных значениях постоянных .

Замечания:

3) Для нахождения частного решения уравнения (1) задают два начальных условия , 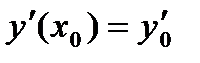. В некоторых задачах используют так называемые краевые условия: задают значения функции на концах некоторого отрезка : .

4) Соотношение вида , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения 2-го порядка.