Двойной интеграл

Задача об объеме цилиндрического бруса Рассмотрим в плоскости ОХY замкнутую

область D, ограниченную линей L. Пусть в области D задана непрерывная функция

Определение. Цилиндрическим брусом называется тело, ограниченное: снизу - областью D, сверху – графиком функции , сбоку – цилиндрической поверхностью, образующие которой параллельны оси Oz.

Требуется найти объем V цилиндрического бруса. Повторяя рассуждения, которые проводились в задаче о площади криволинейной трапеции, приходим к следующей схеме решения:

1) Разобьём область D линиями произвольным образом на n элементарных областей которые будем называть площадками. Будем обозначать через не только названия соответствующих площадок, но и их площади. Обозначим диаметры элементарных областей (диаметром области называется наибольшее из расстояний между двумя точками границы этой области).

2) В каждой из областей выберем точку , тогда будем иметь точки

3) Обозначим через значения функции в выбранных точках.

4) На каждую элементарную область опирается своя часть бруса, заменим его объем приближенно объемом прямого цилиндра с высотой 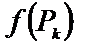и площадью т.е.

5) Объем цилиндрического бруса будет приближенно равен

6) Степень точности вычисления возрастает при измени областей. Пусть тогда точное значение объема цилиндрического бруса будет равно