Интегрирование подстановкой

Положив получим

Такое преобразование интеграла называется интегрированием подстановкой.

Если и то

где

Если числитель подынтегральной функции равен производной ее знаменателя, то интеграл равен логарифму модуля знаменателя плюс произвольная постоянная.

Имеем:

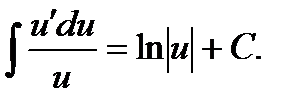
Найти интегралы:

4.

Решение: Данный интеграл берется с помощью и формулы из таблицы основных интегралов.

5.

Решение:

6.

Метод интегрирования по частям.

Интегрирование по частям находится по формуле

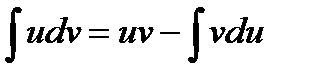
где и дифференцируемые функции от

1) Интегралы вида 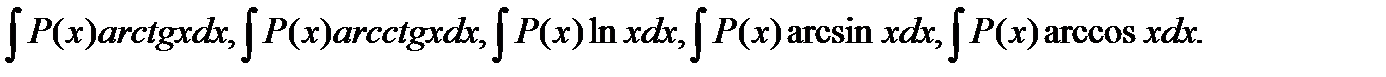где многочлен.

За принимаются соответственно , а за выражение

2) Интегралы вида

где многочлен, а 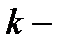некоторое число.

За следует принять а за соответственно выражения

Найти интегралы:

7.

Решение:

8.

Решение: