Практическое занятие № 21,22

Тема: Дифференциальные уравнения первого порядка

Цель занятий: Уметь разделить переменные. Решить дифференциальное уравнения с начальным условием. Однородные и линейные дифференциальные уравнения

Вопросы: 1.Общий вид дифференциального уравнения первого порядка. 2. Общие и частное решение дифференциального уравнения.

Дифференциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций не равна тождественно нулю, то в результате исходного уравнения разделяя на оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

Пример 1. Найти частное решение уравнения.

.

Решение:

Тема: Однородные дифференциальные уравнения.

Уравнение вид называется однородным, если и -однородные функции одного измерения. Функция называется однородной измерения m, если

Однородное уравнение может быть приведено к виду

С помощью подстановки однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции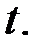

Пример: 1.

Решение:

,

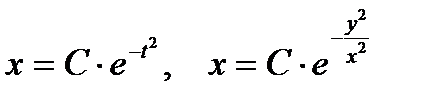
Тема: Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.

Уравнение вида называется линейным ( и входят первых степенях, не перемножаясь между собой).Если то уравнение называется линейным неоднородным, а если -линейным однородным.

Общее решение однородного уравнения легко получается разделением переменных:

или, наконец где С- произвольная постоянная.

Пример1. Решить уравнение

Решение: Это уравнение Бернулли (левая часть у него такая же, как и у линейного, а в правой части стоит выражение 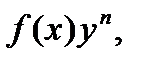где n –постоянное число, в данном примере

Разделим обе части данного уравнения на

Положим тогда Умножая обе части уравнения на –1 и выполняя указанную подстановку, получим линейное уравнение

Решая это уравнение, находим

Следовательно, общим решением данного уравнения будет

Рекомендуемая литература: ОЛ[2], [3], [4], [7],