Первый признак подобия

Теорема. Если два угла одного треугольника соответ­ственно равны двум углам другого, то такие треугольники подобны.

Доказательство

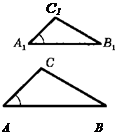
Пусть ∆ АВС и ∆ А₁В₁С₁ — два треугольника, у которых ∠ А=∠ А₁ ∠ В=∠ В₁ (рис. 5). Докажем, что ∆ АВС ~ ∆ A₁B₁C₁.

По теореме о сумме углов тре­угольника ∠ С = 180° - ∠ А - ∠ В, ∠ С₁ =180° - ∠ А₁ - ∠ B₁ и, значит, ∠ С=∠ С₁. Таким об­разом, углы треугольника АВС соответ­ственно равны углам треугольника А₁В₁С₁.

Докажем, что стороны треуголь­ника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Так как ∠ А = ∠ А₁ и ∠ С=∠ С₁, то

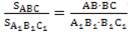
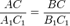
Из этих равенств следует, что. Аналогично, используя ра­венства ∠ А=∠ А₁ ∠ В=∠ В₁, получаем.

Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Теорема доказана.

Второй признак подобия треугольников

Теорема. Если две стороны одного треугольника про­порциональны двум сторонам другого тре­угольника и углы, заключенные между этими сторонами, равны, то такие треуголь­ники подобны.

Доказательство

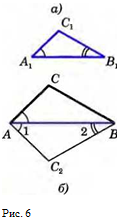Рассмотрим два треугольника АВС и A₁B₁C₁, у которых, ∠ А = ∠ А₁ (рис. 6, а). Докажем, что ∆ АВС ~ ∆ A₁B₁C₁. Для этого, учитывая пер­вый признак подобия треугольников, доста­точно доказать, что ∠ В=∠ В1.

Рассмотрим треугольник АВС₂, у которого ∠ 1 = ∠ А₁, ∠ 2 = ∠ В₁ (рис. 6, б). Треугольники АВС₂ и А₁В₁С₁ подобны по первому признаку подобия треугольников, поэтому

.С другой стороны, по условию.

Из этих двух ра­венств получаем АС=АС₂.

Треугольники АВС и АВС₂ равны по двум сторонам и углу между ними (АВ — общая сторона, АС=АС₂ и ∠ А=∠ 1, по­скольку ∠ А—∠ А₁ и ∠ 1 = ∠ А₁). Отсюда сле­дует, что ∠ В=∠ 2, а так как ∠ 2 = ∠ В₁ то ∠ В = ∠ В₁. Теорема доказана.