Энергия гармонических колебаний.

Рассмотрим систему, на которую действует квазиупругая сила F = –kx. Для того чтобы сообщить системе смещение х, нужно совершить против квазиупругой силы работу

Эта работа идет на создание запаса потенциальной энергии системы. Следовательно, система, в которой действует квазиупругая сила, при смещении из положения равновесия на расстояние х обладает потенциальной энергией

. (144)

Потенциальную энергию в положении равновесия полагаем равной нулю.

Если k – коэффициент жесткости пружины, то формула (144) будет выражать потенциальную энергию сжатой пружины.

Квазиупругая сила является консервативной, поэтому полная энергия гармонического колебания должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно, причем в моменты наибольшего отклонения из положения равновесия полная энергия Е состоит только из потенциальной энергии, которая достигает своего наибольшего значения (144) при
x = x_max.

При прохождении системы через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в эти моменты достигает своего наибольшего значения. Согласно (127), амплитуда скорости равна Aω. Отсюда максимальное значение кинетической энергии:

. (145)

Т. к. k = ω ²m, а при максимальном отклонении x = A, то получается, что максимальное значение кинетической энергии равно максимальному значению потенциальной энергии.

Выясним, как изменяется со временем кинетическая E_k и потенциальная Ep энергия гармонического колебания. Кинетическая энергия равна:

(146)

Потенциальная энергия выражается формулой

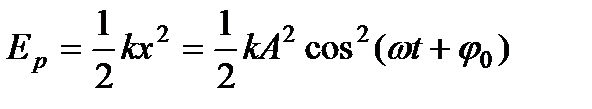(147)

Складывая (146) и (147), учитывая, что k = ω ²m, получим выражение для полной энергии гармонических колебаний:

. (148)

Таким образом, полная энергия гармонических колебаний действительно оказывается постоянной.

Используя известные формулы тригонометрии, выражениям для E_k и E_p можно придать вид:

, (149)

, (150)

где Е – полная энергия системы. Из формул (149) и (150) видно, что Е_k и Е_р изменяются с частотой 2ω, т. е. с частотой, в 2 раза превышающей частоту гармонического колебания.

На рис. 51 сопоставлены графики для х, E_k и Е_р.

Среднее значение квадрата синуса и квадрата косинуса равно 1/2. Следовательно, среднее значение E_k совпадает со средним значением Ер и равно E/2.

Рис. 51.